:某学校举行演讲比赛,选出了10名同学担任评委,并事先拟定从以下4个方案中选择合理的方案来确定每个演讲者的最后得分。
方案1:所有评委所给分的平均数.方案2:在所有评委所给分中,去掉一个最高分和一个最低分,然后再计算其余给分的平均数.
方案3:所有评委所给分的中位数.
方案4:所有评委所给分的众数.
|
为了探究上述方案的合理性,先对某个同学的演讲成绩进行了统计实验.下面是这个同学的得分统计图:

解不等式3x-1<7,将解集在数轴上表示出来,并写出它的非负整数解.
如图,某幢大楼顶部有一块广告牌CD,甲乙两人分别在相距8米的A、B两处测得D点和C点的仰角分别为45°和60°,且A、B、E三点在一条直线上,若BE=15米,求这块广告牌的高度.(取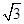 ≈1.73,计算结果保留整数)
≈1.73,计算结果保留整数)
如图,方格纸中的每个小正方形边长都是1个长度单位,Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(1,1),点B的坐标为(4,1).
(1)先将Rt△ABC向左平移5个单位长度,再向下平移1个单位长度得到Rt△A1B1C1,试在图中画出Rt△A1B1C1,并写出点A1的坐标;
(2)再将Rt△A1B1C1绕点A1顺时针旋转90°后得到Rt△A2B2C2,试在图中画出Rt△A2B2C2,并计算Rt△A1B1C1在上述旋转过程中点C1所经过的路径长.
先化简,再求值: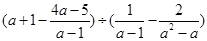 ,其中a=-1.
,其中a=-1.
已知:二次函数y=ax2+bx+6(a≠0)与x轴交于A,B两点(点A在点B的左侧),点A、点B的横坐标是一元二次方程x2-4x-12=0的两个根.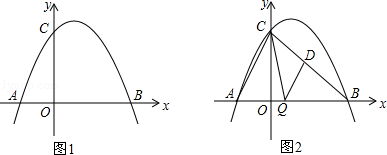
(1)请直接写出点A、B的坐标,并求出该二次函数的解析式.
(2)如图1,在二次函数对称轴上是否存在点P,使△APC的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
(3)如图2,连接AC、BC,点Q是线段OB上一个动点(点Q不与点O、B重合).过点Q作QD∥AC交BC于点D,设Q点坐标(m,0),当△CDQ面积S最大时,求m的值.