(本题6分)请在右侧网格图中画出所给图形绕点O顺时针依次旋转90°、180°、270°后所成的图形. (注意:有阴影部分图形旋转后的对应图形要涂上阴影,不要求写画法)
(注意:有阴影部分图形旋转后的对应图形要涂上阴影,不要求写画法)

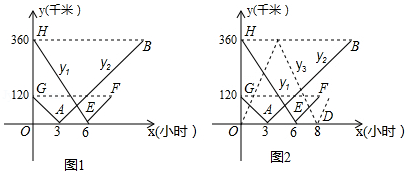
在甲、乙两城市之间有一服务区,一辆客车从甲地驶往乙地,一辆货车从乙地驶往甲地.两车同时出发,匀速行驶,客车、货车离服务区的距离 (千米), (千米)与行驶的时间 (小时)的函数关系图象如图1所示.
(1)甲、乙两地相距 千米.
(2)求出发3小时后,货车离服务区的路程 (千米)与行驶时间 (小时)之间的函数关系式.
(3)在客车和货车出发的同时,有一辆邮政车从服务区匀速去甲地取货后返回乙地(取货的时间忽略不计),邮政车离服务区的距离 (千米)与行驶时间 (小时)之间的函数关系图线如图2中的虚线所示,直接写出在行驶的过程中,经过多长时间邮政车与客车和货车的距离相等?
我市某中学为了了解孩子们对《中国诗词大会》,《挑战不可能》,《最强大脑》,《超级演说家》,《地理中国》五种电视节目的喜爱程度,随机在七、八、九年级抽取了部分学生进行调查(每人只能选择一种喜爱的电视节目),并将获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据两幅统计图中的信息回答下列问题:
(1)本次调查中共抽取了 名学生.
(2)补全条形统计图.
(3)在扇形统计图中,喜爱《地理中国》节目的人数所在的扇形的圆心角是 度.
(4)若该学校有2000人,请你估计该学校喜欢《最强大脑》节目的学生人数是多少人?

如图, 的直角边 在 轴上, , ,将 绕点 逆时针旋转 得到 ,抛物线 经过 、 两点.
(1)求二次函数的解析式;
(2)连接 ,点 是抛物线上一点,直线 把 的周长分成相等的两部分,求点 的坐标.

如图,在平面直角坐标系中, 的三个顶点都在格点上,点 的坐标为 请解答下列问题:
(1)画出 关于 轴对称的△ ,并写出 的坐标.
(2)画出 绕点 逆时针旋转 后得到的△ ,并写出 的坐标.
(3)画出△ 关于原点 成中心对称的△ ,并写出 的坐标.

已知:如图,直线 与 轴负半轴交于点 ,与 轴正半轴交于点 ,线段 的长是方程 的一个根,请解答下列问题:
(1)求点 坐标;
(2)双曲线 与直线 交于点 ,且 ,求 的值;
(3)在(2)的条件下,点 在线段 上, ,直线 轴,垂足为点 ,点 在直线 上,坐标平面内是否存在点 ,使以 、 、 、 为顶点的四边形是矩形?若存在,请直接写出点 的坐标;若不存在,请说明理由.
