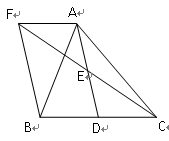
(本题8分)阅读下列材料:若关于 的一元二次方程
的一元二次方程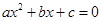
 的两个实数根分别为
的两个实数根分别为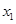 、
、 ,则
,则 ,
, 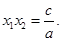
解决下面问题:已知关于x的一元二次方程 有两个非零不等实数根
有两个非零不等实数根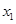 、
、 ,设
,设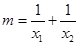 .
.(1) 求
 的取值范围;
的取值范围;(2) 试用关于
 的代数式表示出
的代数式表示出 ;
;(3) 是否存在这样的
 值,使
值,使 的值等于1?若存在,求出这样的所有
的值等于1?若存在,求出这样的所有 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题8分)如图,点A、B、C、D在⊙O上,AD为 ⊙O的直径,AD = 6cm,∠DAC =∠B,求AC的长.


(3)画出△ABC以点C为旋转中心、旋转180°后的△A′B′C′.
正方形ABCD与正方形CEFG的位置如图所示,点G在线段CD或CD的延长线上. 分别连接BD,BF,FD,得到△BFD.
(1)在图中,若正方形CEFG的边长分别为1,3,4,且正方形ABCD的边长均为3,请通过计算填写下表:
正方形CEF G的边长 G的边长 |
1 |
3 |
4 |
| △BFD的面积 |
(2)若正方形CEFG的边长为a,正方形ABCD的边长为b,猜想S△BFD的大小,并结合图3证明你的猜想.
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
(1)求证:D是BC的中点.
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.