从4名书法比赛一等奖的同学和2名绘画比赛一等奖的同学中选出2名志愿者,参加某项服务工作.
(1)求选出的两名志愿者都是获得书法比赛一等奖的同学的概率;
(2)求选出的两名志愿者中一名是获得书法比赛一等奖,另一名是获得绘画比赛一等奖的同学的概率.
(本小题12分)已知函数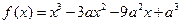 .
.
(1)设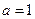 ,求函数
,求函数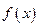 的极值;
的极值;
(2)若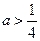 ,且当
,且当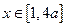 时,
时,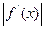
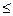 12a恒成立,试确定
12a恒成立,试确定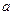 的取值范围.
的取值范围.
已知二次函数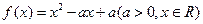 ,不等式
,不等式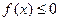 的解集有且只有一个元素,设数列
的解集有且只有一个元素,设数列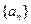 的前
的前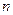 项和
项和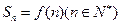
(1)求数列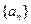 的通项公式;
的通项公式;
(2)设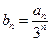 ,求数列
,求数列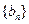 的前
的前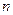 项和
项和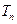 .
.
如图,三棱柱ABC—A1B1C1中,AA1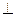 面ABC,BC
面ABC,BC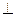 AC,BC=AC=2,D为AC的中点。
AC,BC=AC=2,D为AC的中点。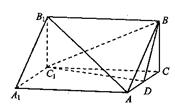
(1)求证:AB1//面BDC1;
(2)若AA1=3,求二面角C1—BD—C的余弦值;
(3)若在线段AB1上存在点P,使得CP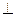 面BDC1,试求AA1的长及点P的位置。
面BDC1,试求AA1的长及点P的位置。
甲、乙、丙三台机床各自独立的加工同一种零件,已知甲、乙、丙三台机床加工的零件是一等品的概率分别为0.7、0.6、0.8,乙、丙两台机床加工的零件数相等,甲机床加工的零件数是乙机床加工的零件数的二倍.
(1)从甲、乙、丙加工的零件中各取一件检验,求至少有一件一等品的概率;
(2)将三台机床加工的零件混合到一起,从中任意的抽取一件检验,求它是一等品的概率;
(3)将三台机床加工的零件混合到一起,从中任意的抽取4件检验,求一等品的个数不少于3个的概率。
设函数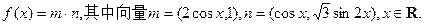
(1)求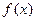 的最小正周期与单调递减区间;
的最小正周期与单调递减区间;
(2)在△ABC中,a、b、c分别是角A、B、C的对边,已知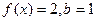 ,△ABC的面积为
,△ABC的面积为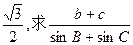 的值。
的值。