已知抛物线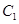 :
: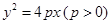 ,焦点为
,焦点为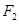 ,其准线与
,其准线与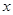 轴交于点
轴交于点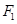 ;椭圆
;椭圆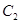 :分别以
:分别以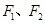 为左、右焦点,其离心率
为左、右焦点,其离心率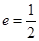 ;且抛物线
;且抛物线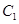 和椭圆
和椭圆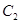
 的一个交点记为
的一个交点记为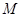 .
.
(1)当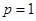 时,求椭圆
时,求椭圆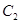 的标准方程;
的标准方程;
(2)在(1)的条件下,若直线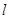 经过椭圆
经过椭圆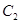 的右焦点
的右焦点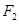 ,且
,且 与抛物线
与抛物线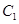 相交于
相交于 两点,若弦长
两点,若弦长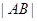 等于
等于 的周长,求直线
的周长,求直线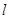 的方程
的方程 .
.
对某校学生进行心理障碍测试得到如下列联表.
| 焦虑 |
说谎 |
懒惰 |
总计 |
|
| 女生 |
5 |
10 |
15 |
30 |
| 男生 |
20 |
10 |
50 |
80 |
| 总计 |
25 |
20 |
65 |
110 |
试说明在这三种心理障碍中哪一种与性别关系最大?
从甲、乙两种玉米苗中各抽10株,分别测得它们的株高如下(单位:cm)
甲:25 41 40 37 22 14 19 39 21 42
乙:27 16 44 27 44 16 40 40 16 40
问:(1)哪种玉米的苗长得高?
(2)哪种玉米的苗长得齐?
甲、乙两个车间分别制作一种零件,在自动包装传送带上每隔10分钟抽取一件产品,测其质量,分别记录抽查的数据如下:
甲:102, 101, 99, 98, 103, 98, 99;
乙:105, 102, 97, 92, 96, 101, 107;
(1)这种抽样方法是什么抽样?
(2)估计甲、乙两个车间产品质量的平均值与方差,并分析哪个车间的产品较稳定;
(3)如果产品质量在区间(95,105)内为合格,那么这个工厂生产的产品合格率是多少?
某重点中学高中各班级学生人数如下表所示:
| 年级 班 |
高一年级 |
高二年级 |
高三年级 |
| 1班 |
45 |
46 |
48 |
| 2班 |
48 |
54 |
55 |
| 3班 |
52 |
50 |
52 |
学校计划召开学生代表座谈会.请根据上述基本数据,设计一个容量为总体容量的 的抽样方案.
的抽样方案.
在调查的480名男人中有38名患有色盲,520名女人中有6名患有色盲,分别利用图形和独立性检验的方法来判断色盲与性别是否有关?你所得到的结论在什么范围内有效?