某重点中学高中各班级学生人数如下表所示:
| 年级 班 |
高一年级 |
高二年级 |
高三年级 |
| 1班 |
45 |
46 |
48 |
| 2班 |
48 |
54 |
55 |
| 3班 |
52 |
50 |
52 |
学校计划召开学生代表座谈会.请根据上述基本数据,设计一个容量为总体容量的 的抽样方案.
的抽样方案.
已知某海滨浴场的海浪高达y(米)是时间t(0≤t≤24,单位:小时)的函数,记作y=f(t).下表是某日各时的浪高数据.
| t(时) |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
| y(米) |
1.5 |
1.0 |
0.5 |
1.0 |
1.5 |
1.0 |
0.5 |
0.99 |
1.5 |
经长期观测,y=f(t)的曲线可近似地看成是函数y=Acosωt+b.
(1)根据以上数据,求出函数y=Acosωt+b的最小正周期T、振幅A及函数表达式;
(2)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午8:00至晚上20:00之间,有多长时间可供冲浪者进行运动?
平面直角坐标系xOy内有向量 =(1,7),
=(1,7),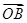 =(5,1),
=(5,1), =(2,1),点Q为直线OP上一动点.
=(2,1),点Q为直线OP上一动点.
(1)当 ·
·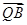 取得最小值时,求
取得最小值时,求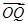 坐标;
坐标;
(2)当点Q满足(1)中条件时,求cos∠AQB的值.
(1)已知α是第一象限的角,且cosα=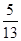 ,求
,求 的值.
的值.
(2)化简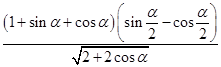 ,其中π<α<2π.
,其中π<α<2π.
设定义在 上的函数
上的函数 ,满足当
,满足当 时,
时, ,且对任意
,且对任意 ,有
,有 ,
,
(1)解不等式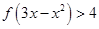
(2)解方程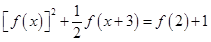
已知函数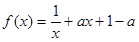 ,
, ,
,
(1)若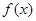 为奇函数,求
为奇函数,求 的值;
的值;
(2)若 =1,试证
=1,试证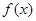 在区间
在区间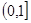 上是减函数;
上是减函数;
(3)若 =1,试求
=1,试求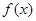 在区间
在区间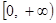 上的最小值.
上的最小值.