记等差数列{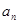
}的前n项和为
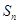，已知
，
．
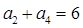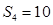（Ⅰ）求数列{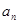}的通项公式；
（Ⅱ）令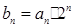
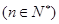，求数列{
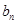}的前项和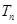
．
．(本题满分10分)
已知函数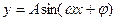
（
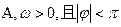）在一个周期内的图象如图，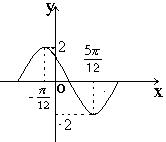
(Ⅰ) 求函数的解析式。
(Ⅱ)求函数的单调递增区间。
若平面内给定三个向量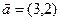
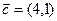
（1）求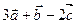
。
（2）求满足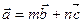
的实数m，n的值。
．(本小题满分12分)
已知函数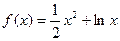
．
（1）求函数
在区间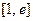
上的最大值、最小值；
（2）已知
，求证：在区间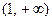
上，函数的图象在函数
的图
象的下方．
（本小题满分12分）
数列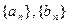
满足：
（1）求数列
的通项公式；（2）设数列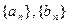的前n项和分别为An、Bn，问是否存在实数
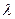，使得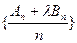
为等差数列？若存在，求出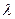的值；若不存在，说明理由。
（本小题满分12分）
一项"过关游戏"规则规定: 在第n 关要抛掷骰子n次, 若这n次抛掷所出现的点数之和大于
＋1 (n∈N*), 则算过关.
(1)求在这项游戏中第三关过关的概率是多少?
(2)若规定n≤3, 求某人的过关数ξ的期望.