已知椭圆C: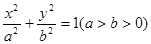 的一条准线L方程为:x=
的一条准线L方程为:x=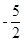 ,且左焦点F到L的距离为
,且左焦点F到L的距离为 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点F的直线交椭圆C于两点A、B,交L于点M,若 ,
,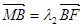 ,证明
,证明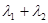 为定值.
为定值.
已知a, b都是正数,并且a ¹ b,求证:a5 + b5 > a2b3 + a3b2
正数a,b,c满足a+b+c=1,求证:(1-a)(1-b)(1-c)≥8abc。
设函数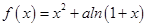 有两个极值点
有两个极值点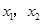 ,且
,且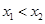 .
.
(1)求 的取值范围,并讨论
的取值范围,并讨论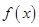 的单调性;
的单调性;
(2)证明: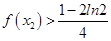 .
.
已知函数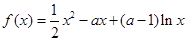 ,
, .
.
(1)讨论函数 的单调性;
的单调性;
(2)证明:若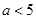 ,则对任意
,则对任意 ,
, ,有
,有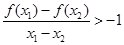 .
.
已知圆 和点
和点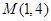 .
.
(1)过点M向圆O引切线,求切线的方程;
(2)求以点M为圆心,且被直线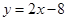 截得的弦长为8的圆M的方程;
截得的弦长为8的圆M的方程;
(3)设P为(2)中圆M上任意一点,过点P向圆O引切线,切点为Q,试探究:平面内是否存在一定点R,使得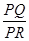 为定值?若存在,请求出定点R的坐标,并指出相应的定值;若不存在,请说明理由.
为定值?若存在,请求出定点R的坐标,并指出相应的定值;若不存在,请说明理由.