(本小题共13分)某市医疗保险实行定点医疗制度,按照“就近就医、方便管理”的原则,参加保险人员可自主选择四家医疗保险定点医院和一家社区医院作为本人就诊的医疗机构.若甲、乙、丙、丁4名参加保险人员所在地区附近有A,B,C三家社区医院,并且他们的选择是相互独立的.
(Ⅰ)求甲、乙两人都选择A社区医院的概率;
(Ⅱ)求甲、乙两人不选择同一家社区医院的概率;
(Ⅲ)设4名参加保险人员中选择A社区医院的人数为ξ,求ξ的分布列和数学期望.
关于 的不等式
的不等式 在区间
在区间 上有解,求
上有解,求 的取值范围.
的取值范围.
解不等式: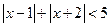
已知函数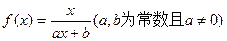 满足
满足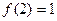 ,且
,且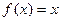 有唯
有唯
一实数解。
(1)求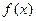 的表达式 ;
的表达式 ;
(2)记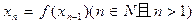 ,且
,且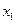 =
=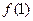 ,求数列
,求数列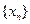 的通项公式。
的通项公式。
(3)记 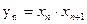 ,数列{
,数列{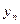 }的前
}的前 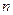 项和为
项和为 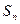 ,是否存在k∈N*,使得
,是否存在k∈N*,使得
对任意n∈N*恒成立?若存在,求出k的最小值,若不存在,请说明理由.
已知数列{an}的前n项和为Sn,且an是Sn与2的等差中项,数列{bn}中,b1=1,点P(bn,bn+1)在直线 上。
上。
(1)求a1和a2的值;
(2)求数列{an},{bn}的通项an和bn;
(3)设cn=an·bn,求数列{cn}的前n项和Tn.
某外商到一开发区投资72万美元建起一座蔬菜加工厂,第一年各种经费12万美元,以后每年增加4万美元,每年销售蔬菜收入50万美元。
(1)若扣除投资及各种经费,则从第几年开始获取纯利润?
(2)若干年后,外商为开发新项目,按以下方案处理工厂:纯利润总和最大时,以16万美元出售该厂,问多长时间可以出售该工厂?能获利多少?