(3)若正数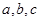 满足
满足 ,求
,求 的最小值。
的最小值。
设函数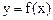 是定义在
是定义在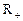 上的函数,并且满足下面三个条件:(1)对正数x、y都有
上的函数,并且满足下面三个条件:(1)对正数x、y都有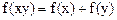 ;(2)当
;(2)当 时,
时, ;(3)
;(3) 。则
。则
(Ⅰ)求 和
和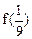 的值;
的值;
(Ⅱ)如果不等式 成立,求x的取值范围.
成立,求x的取值范围.
(Ⅲ)如果存在正数k,使不等式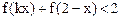 有解,求正数
有解,求正数 的取值范围.
的取值范围.
在如图所示的几何体中.EA⊥平面ABC,
DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M是AB的中点.
(Ⅰ)求证:CM⊥EM ;
(Ⅱ)求多面体ABCDE的体积
(Ⅲ)求直线DE与平面EMC所成角的正切值.
如图,已知底角为45°的等腰梯形ABCD,底边BC长为7 cm,腰长为2 cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出左边部分的面积y与x的函数解析式,并画出大致图象.
cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出左边部分的面积y与x的函数解析式,并画出大致图象.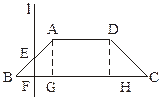
二次函数f(x)满足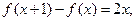 且f(0)=1.
且f(0)=1.
(1)求f(x)的解析式;
(2)若在区间 上, 不等式f(x)
上, 不等式f(x) 2x+m恒成立,求实数m的范围.
2x+m恒成立,求实数m的范围.
已知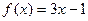 ,
, ,
, 为
为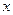 的一次函数,求
的一次函数,求