设函数 。若函数
。若函数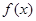 在
在 处与直线
处与直线 相切,
相切,
(1)求实数 ,b的值;(2)求函数
,b的值;(2)求函数 上的最大值;
上的最大值;
已知等差数列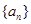 的公差
的公差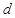 大于0,且
大于0,且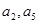 是方程
是方程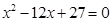 的两根,数列
的两根,数列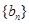 的前
的前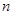 项和为
项和为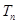 ,且
,且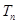
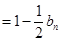
(1)求数列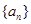 、
、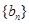 的通项公式;
的通项公式;
(2)设数列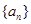 的前
的前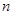 项和为
项和为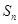 ,试比较
,试比较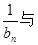
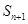 的大小,并说明理由.
的大小,并说明理由.
双曲线 上一点
上一点 到左,右两焦点距离的差为2.
到左,右两焦点距离的差为2.
(1)求双曲线的方程;
(2)设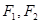 是双曲线的左右焦点,
是双曲线的左右焦点,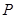 是双曲线上的点,若
是双曲线上的点,若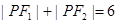 ,
,
求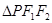 的面积;
的面积;
(3)过 作直线
作直线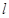 交双曲线
交双曲线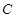 于
于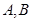 两点,若
两点,若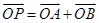 ,是否存在这样的直线
,是否存在这样的直线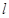 ,使
,使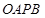 为矩形?若存在,求出
为矩形?若存在,求出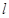 的方程,若不存在,说明理由.
的方程,若不存在,说明理由.
如图,三棱柱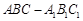 中,侧面
中,侧面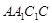
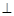 底面
底面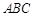 ,
,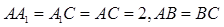 ,且
,且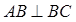 ,O为
,O为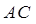 中点.
中点.
(1)证明: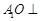 平面
平面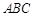 ;
;
(2)求直线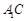 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(3)在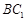 上是否存在一点
上是否存在一点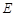 ,使得
,使得 平面
平面 ,
,
若不存在,说明理由;若存在,确定点 的位置.
的位置.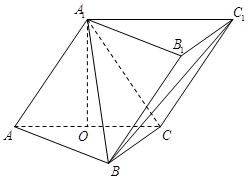
解关于 的不等式:
的不等式:
在△ABC中,角A,B,C所对的边分别为a,b,c,且满足csinA=acosC.
(1)求角C的大小;
(2)求 的最大值,并求取得最大值时角A、B的大小.
的最大值,并求取得最大值时角A、B的大小.