已知椭圆
，
分别为左顶点和上顶点，F为右焦点，过F作
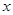轴的垂线交椭圆于点C，且直线
与直线OC平行.
（1）求椭圆的离心率；
（2）已知定点M（
），
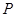为椭圆上的动点，若
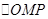的重心轨迹经过点
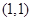，求椭圆的方程.
(10分) 解不等式|x-2|+|x-3|<9
(10分)设复数z=m+1+(m-1)i，试求m取何值时
（1）Z是实数；
（2）Z是虚数；
（3）Z对应的点位于复平面的第一象限
选修4—5；不等式选讲
已知a和b是任意非零实数.
（1）求
的最小值.
（2）若不等式
恒成立，求实数x的取值范围.
选修4—4;坐标系与参数方程
在平面直角坐标系xOy中，已知曲线
，以平面直角坐标系xOy的原点O为极点，x轴的正半轴为极轴，取相同的单位长度建立极坐标系，已知直线
.
（1）将曲线
上的所有点的横坐标、纵坐标分别伸长为原来的
、2倍后得到曲线
试写出直线
的直角坐标方程和曲线的参数方程；
（2）在曲线上求一点P，使点P到直线的距离最大，并求出此最大值.
选修4－1：几何证明选讲
在
中，AB=AC，过点A的直线与其外接圆交于点P，交BC延长线于点D.
（1）求证：
；
（2）若AC=3，求
的值.