先化简再求值(2a+b) 2－(3a－b) 2+5a(a－b)，其中
，
．
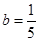解方程组或不等式组：
（1）
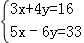
（2）
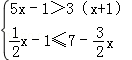并把解集表示在数轴上
（3）
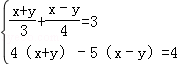
（4）
．
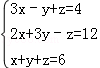在眉山市开展城乡综合治理的活动中，需要将A、B、C三地的垃圾50立方米、40立方米、50立方米全部运往垃圾处理场D、E两地进行处理．已知运往D地的数量比运往E地的数量的2倍少10立方米．
（1）求运往两地的数量各是多少立方米？
（2）若A地运往D地a立方米（a为整数），B地运往D地30立方米，C地运往D地的数量小于A地运往D地的2倍．其余全部运往E地，且C地运往E地不超过12立方米，则A、C两地运往D、E两地哪几种方案？
（3）已知从A、B、C三地把垃圾运往D、E两地处理所需费用如下表：
| A地 |
B地 |
C地 |
|
| 运往D地（元/立方米） |
22 |
20 |
20 |
| 运往E地（元/立方米） |
20 |
22 |
21 |
在（2）的条件下，请说明哪种方案的总费用最少？
现计划把甲种货物1240吨和乙种货物880吨用一列货车运往某地，已知这列货车挂有A、B两种不同规格的货车厢共40节，使用A型车厢每节费用为6000元，使用B型车相每节费用为8000元．
（1）设运送这批货物的总费用为y万元，这列货车挂A型车厢x节，试写出y与x之间的函数关系式；
（2）如果每节A型车厢最多可装甲种货物35吨和乙种货物15吨，每节B型车厢最多可装甲种货物25吨和乙种货物35吨，装货时按此要求安排A、B两种车厢的节数，那么共有哪几种安排车厢的方案？
（3）在上述方案中，哪个方案运费最省最少运费为多少元？
如图，在平面直角坐标系中，二次函数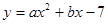
的图象交x轴于
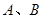两点，交
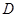轴于点
，点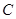
为抛物线的顶点，且
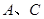两点的横坐标分别为1和4．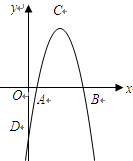
（1）求点B的坐标；
（2）求二次函数的函数表达式；
（3）在（2）的抛物线上，是否存在点P，使得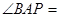
45°？若存在，求出点P的坐标；若不存在，请说明理由．
如图，BC是⊙O的直径，A是弦BD延长线上一点，切线DE平分AC于E。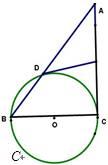
（1）求证：AC是⊙O的切线；
（2）若AD:DB=3:2，AC=15，求⊙O的直径。