(本题8分)某中学九(1)班同学积极响应“阳光体育工程”的号召,利用课外活动时间积极参加体育锻炼,每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练,训练前后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图表.
请你根据图表中的信息回答下列问题:(1)训练后篮球定时定点投篮人均进球数为 ▲ ;
(2)选择长跑训练的人数占全班人数的百分比是 ▲ ,该班共有同学 ▲ 人;
(3)根据测试资料,训练后篮球定时定点投篮的人均进球数比训练之前人均进球数增加25% ,请求出参加训练之前的人均进球数.
根据下列条件求出∠A的度数:
(1)sinA=0.6031; (2)cosA=0.3215; (3)tanA=0.2136;
(4)sinA=0.37; (5)cosA=0.63; (6)tanA=3.465.
用计算器求下列各式的值:
(1)sin20°; (2)cos38°;(3)tan10°;(4)tan80°;
(5)cos27°51′;(6)tan56°17′35″; (7)sin75°31′12″; (8)3sin29°.
如图,点A的坐标是(0.5,0),现在点A绕着点O按逆时针方向旋转, 每秒钟旋转30°,同时点A离开O点的距离以每秒0.5个单位的速度在增大,当A点第11 秒钟时到达图中的P点处,求P点的坐标.

某学生站在公园湖边的M处,测得湖心亭A位于北偏东30°方向上,又测得游船码头B位于南偏东60°方向上.现有一艘游船从湖心亭A 处沿正南方向航行返回游船码头,已知M处与AB的距离MN=0.7千米,求湖心亭与游船码头B的距离(精确到0.1千米).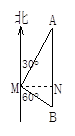
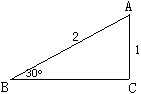
要求tan30°的值,可构造如图所示的直角三角形进行计算.
作Rt△ABC,使∠C=90°,斜边AB=2,直角边AC=1,那么BC= ,∠ABC=" 30" °
,∠ABC=" 30" °
∴tan30°= .
.
在此图的基础上,通过添加适当的辅助线,可求出tan15°的值,请简要写出你添加的辅助线和求出的tan15°的值.