（本题12分）已知：如图，二次函数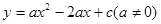
的图象与y轴交于点C（0，4），与x轴交于点A、B，点A的坐标为（4，0）.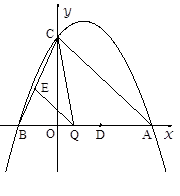
（1）求该二次函数的关系式；
（2）写出该二次函数的对称轴和顶点坐标；
（3）点Q是线段AB上的动点，过点Q作QE∥AC，交BC于点E，连接CQ.当△CQE的面积最大时，求点Q的坐标；
（4）若平行于x轴的动直线
与该抛物线交于点P，与直线AC交于点F，点D的坐标为（2，0）.问：是否存在这样的直线，使得△ODF是等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由。
解下列方程：
(1) 3
－2＝4＋5
(2)＋
＝3－
（1）计算：
÷
（2）化简：
如图是一个玩具火车轨道，点A有个变轨开关，可以连接点B或点C.小圈轨道的周长是2米，大圈轨道的周长是4米.开始时，点A连接点C，火车从点A出发，按照顺时针方向在轨道上移动，同时变轨开关每隔一分钟变换一次轨道连接.若火车的速度是每分钟10米，则火车第10次回到A点时用了分钟.
如图，∠BAD=∠CAE=90o，AB=AD，AE=AC， AF⊥CF，垂足为F 
（1）若AC=10，求四边形ABCD的面积；
（2）求证：AC平分∠ECF；
（3）求证：CE="2AF"
某文具店老板第一次用1000元购进一批文具，很快销售完毕；第二次购进时发现每件文具进价比第一次上涨了2 5元。老板用2500元购进了第二批文具，所购进文具的数量是第一次购进数量的2倍，同样很快销售完毕，两批文具的售价均为每件15元。
（1）问第二次购进了多少件文具？
（2）文具店老板第一次购进的文具有3% 的损耗，第二次购进的文具有5% 的损耗，问文具店老板在这两笔生意中是盈利还是亏本？请说明理由。