(本小题满分12分)为了解某班学生喜爱打篮球是否与性别有关，对本班50人进行了问卷调查得到了如下的列联表：
| |
喜爱打篮球 |
不喜爱打篮球 |
合计 |
| 男生 |
|
5 |
|
| 女生 |
10 |
|
|
| 合计 |
|
|
50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为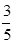
．
（1）请将上面的列联表补充完整(不用写计算过程)；
（2）能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关？说明你的理由；
（3）现从女生中抽取2人进一步调查，设其中喜爱打篮球的女生人数为
，求的分布列与期望.
下面的临界值表供参考：
 |
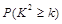0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
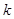2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式：
，其中
)
已知函数
的部分图象如图所示：
（1）求
，
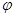的值；
（2）设函数
，当
时，求函数
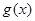的值域．
某良种培育基地正在培育一种小麦新品种A，种植了25亩，所得亩产数据（单位：千克）如下：
363，371，374，383，385，386，391，392，394，394，395，397，397，400，401，401，403，406，407，410，412，415，416，422，430．
（1）求这二十五个数据的中位数；
（2）以组距为10进行分组，完成答题卡上的品种A亩产量的频率分布表；
| 分组 |
频数 |
频率 |
 |
||
 |
||
 |
||
 |
||
 |
||
 |
||
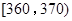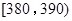| [420，430] |
||
| 合计 |
完成答题卡上的品种A亩产量的频率分布直方图．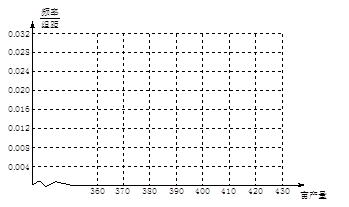
如图：已知扇形
所在圆半径为1，
,扇形内接矩形
，设
．
（1）将矩形面积S表示为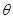
的函数，并指出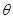的取值范围；
（2）当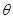取何值时，矩形面积S最大，并求S的最大值．
集合A是由适合以下性质的函数f(x)构成的：对于定义域内任意两个不相等的实数
，都有
．
（1）试判断f(x)= x2及g(x)=log2x是否在集合A中，并说明理由；
（2）设f(x)ÎA且定义域为(0，+¥)，值域为(0，1)，
，试求出一个满足以上条件的函数f (x)的解析式．
（本小题满分14分）已知
，设
：函数
在R上单调递减；
：函数
的图象与x轴至少有一个交点．如果P与Q有且只有一个正确，求
的取值范围．