.(本小题满分14分)已知椭圆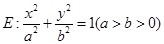 上的点
上的点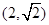 到两个焦点的距离之和为
到两个焦点的距离之和为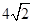 。
。
(Ⅰ)求椭圆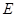 的方程;
的方程;
(Ⅱ)若直线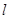 与椭圆
与椭圆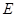 交于两点
交于两点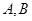 ,且
,且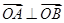 (
(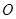 为坐标原点),求
为坐标原点),求 的最大值和最小值。
的最大值和最小值。
已知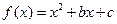 为偶函数,曲线
为偶函数,曲线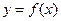 过点
过点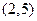 ,
,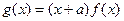 .
.求曲线
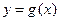 有斜率为0的切线,求实数
有斜率为0的切线,求实数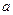 的取值范围;
的取值范围;若当
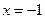 时函数
时函数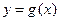 取得极值,确定
取得极值,确定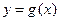 的单调区间.
的单调区间.
某单位为绿化环境,移栽了甲、乙两种大树各2株.设甲、乙两种大树移栽的成活率分别为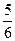 和
和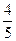 ,且各株大树是否成活互不影响.求移栽的4株大树中:
,且各株大树是否成活互不影响.求移栽的4株大树中:至少有1株成活的概率;
两种大树各成活1株的概率
在五面体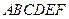 中,
中,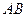 ∥
∥ ,
,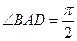 ,
, ,四边形
,四边形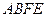 为平行四边形,
为平行四边形,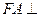 平面
平面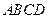 ,
, .求:
.求:直线
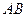 到平面
到平面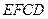 的距离;
的距离;二面角
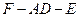 的平面角的正切
的平面角的正切
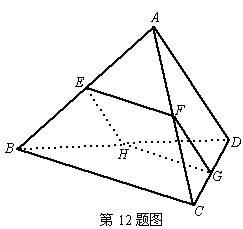
空间四边形ABCD的对棱AD,BC成60°的角,且AD=BC=a,平行于AD与BC的截面分别交AB,AC,CD,BD于E、F、G、H.求证:四边形EFGH为平行四边形;
E在AB的何处时截面EFGH的面积最大?最大面积是多少?
在正方体ABCD—A1B1C1D1中,E,F分别是棱BC,C1D1的中点,求证;EF∥平面BB1D1D.