如图,在梯形 中
中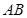 ‖
‖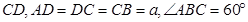 ,平面
,平面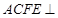 平面
平面 ,四边形
,四边形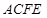 是矩形,
是矩形,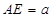 ,点
,点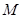 在线段
在线段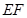 上.
上.
(Ⅰ)求证: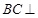 平面
平面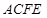 ;
;
(Ⅱ)当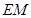 为何值时,
为何值时,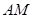 ‖平面
‖平面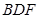 ?证明你的结论;
?证明你的结论;
(Ⅲ)求二面角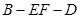 的大小.
的大小. 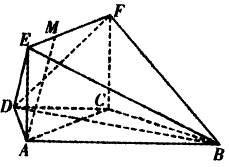
某班同学利用五一节进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念,则称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
| 组数 |
分组 |
低碳族 的人数 |
占本组 的频率 |
| 1 |
[25,30) |
120 |
0.6 |
| 2 |
[30,35) |
195 |
P |
| 3 |
[35,40) |
100 |
0.5 |
| 4 |
[40,45) |
a |
0.4 |
| 5 |
[45,50) |
30 |
0.3 |
| 6 |
[50,55) |
15 |
0.3 |
(1)请补全频率分布直方图,并求n、a、p的值;
(2)在所得样本中,从[40,50)岁年龄段的“低碳族”中采用分层抽样法抽取18人参加户外低碳体验活动,其中选取3人作为领队,记选取的3名领队中年龄在[40,45)岁的人数为X,求X的分布列和数学期望EX.
已知 ,分别求f(0)+f(1),f(﹣1)+f(2),f(﹣2)+f(3),然后归纳猜想一般性结论,并证明你的结论.
,分别求f(0)+f(1),f(﹣1)+f(2),f(﹣2)+f(3),然后归纳猜想一般性结论,并证明你的结论.
若数列 满足
满足 ,则称数列
,则称数列 为“平方递推数列”.已知数列
为“平方递推数列”.已知数列 中,
中, ,点
,点 在函数
在函数 的图象上,其中
的图象上,其中 为正整数.
为正整数.
(1)证明数列 是“平方递推数列”,且数列
是“平方递推数列”,且数列 为等比数列;
为等比数列;
(2)设(1)中“平方递推数列”的前 项积为
项积为 ,即
,即 ,求
,求 ;
;
(3)在(2)的条件下,记 ,求数列
,求数列 的前
的前 项和
项和 ,并求使
,并求使 的
的 的最小值.
的最小值.
如图,公园要把一块边长为 的等边三角形
的等边三角形 的边角地修成草坪,
的边角地修成草坪, 把草坪分成面积相等的两部分,
把草坪分成面积相等的两部分, 在
在 上,
上, 在
在 上.
上.
(1)设 ,
, ,试用
,试用 表示函数
表示函数 ;
;
(2)如果 是灌溉水管,希望它最短,
是灌溉水管,希望它最短, 的位置应该在哪里?
的位置应该在哪里?
关于 的方程
的方程 的两根分别在区间
的两根分别在区间 与
与 内,求
内,求 的取值范围.
的取值范围.