如图所示,己知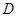 为
为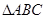 的
的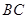 边上一点,
边上一点,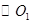 经过点
经过点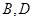 ,交
,交 于另一点
于另一点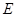 ,
, 经过点
经过点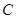 ,
,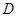 ,交
,交 于另一点
于另一点 ,
, 与
与 的另一交点为
的另一交点为 .
.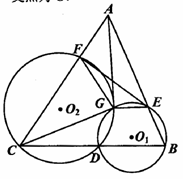
(I)求证: 四点共圆;
四点共圆;
(II)若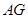 切
切 于
于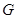 ,求证:
,求证: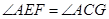 .
.
为考察某种甲型H1N1疫苗的效果,进行动物实验,得到如下疫苗效果的实验列联表:
| 感染 |
 未感染 未感染 |
总计 |
|
| 没服用 |
20 |
30 |
50 |
| 服用 |
x |
y |
50 |
| 总计 |
M |
N |
100 |
设从没服用疫苗的动物中任取两只,感染数为 从服从过疫苗的动物中任取两只,感染数为
从服从过疫苗的动物中任取两只,感染数为 工作人员曾计算过
工作人员曾计算过
 (
( 1)求出列联表中数据
1)求出列联表中数据 的值;
的值;
(2)写出 的均值(不要求计算过程),并比较大小,请解释所得出的结论的实际意义;
的均值(不要求计算过程),并比较大小,请解释所得出的结论的实际意义;
(3)能够以97.5%的把握认为这种甲型H1N1疫苗有效么?并说明理由。
参考公式:
 参考数据:
参考数据:
 |
0.05 |
0.025 |
0.010 |
 |
3.841 |
5.024 |
6.635 |
. (本小题满分12分)
(本小题满分12分)
如图,四边形ABCD为正方形,PD 平面ABCD,PD=AD=2。
平面ABCD,PD=AD=2。
(1)求PC与平面PBD所成的角;
(2)在线段PB上是否存在一点E,使得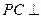 平面ADE?并说明理由。
平面ADE?并说明理由。
(本小题满分12分)
数列 满足:
满足: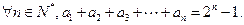
(1)求数列 的通项公式
的通项公式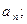
(2)令 ,
, 求数列
求数列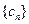 的前n项和
的前n项和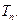
已知函数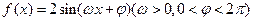 在一个周期内的图象如图所示。
在一个周期内的图象如图所示。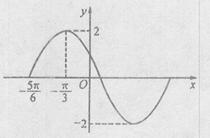
(1)求 的值
的值 ;
;
(2)在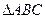 中,设内角A、B、C所对边的长分别为a、b、c。
中,设内角A、B、C所对边的长分别为a、b、c。
若 ,求b的值。
,求b的值。
如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D、E分别在棱PB、PC上,且DE∥BC.
(1)求证:BC⊥平面PAC;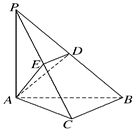 (2)当D为PB的中点时,求AD与平面PAC所成的角的正弦值;
(2)当D为PB的中点时,求AD与平面PAC所成的角的正弦值;
(3)是否存在点E使得二面角A-DE-P为直二面角?并说明理由.