、设函数f(x) = x2+bln(x+1),
(1)若对定义域的任意x,都有f(x)≥f(1)成立,求实数b的值;
(2)若函数f(x)在定义域上是单调函数,求实数b的取值范围;
(3)若b=-1,证明对任意的正整数n,不等式 成立;
成立;
(12 分)已知椭圆
分)已知椭圆 ,直线l与椭圆交于A、B两点,M是线段AB的中点,连接OM并延长交椭圆于点C.直线AB与直线OM的斜率分别为k、m,且
,直线l与椭圆交于A、B两点,M是线段AB的中点,连接OM并延长交椭圆于点C.直线AB与直线OM的斜率分别为k、m,且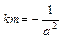 .
.
(Ⅰ)求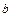 的值;
的值;
(Ⅱ)若直线AB经过椭圆的右焦点F,问:对于任意给定的不等于零的实数k,是否存在a∈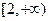 ,使得四边形OACB是平行四边形,请证明你
,使得四边形OACB是平行四边形,请证明你 的结论;
的结论;
已知四棱锥 中,
中, 平面
平面 ,底面
,底面
 是直角梯形,
是直角梯形,
 为
为
 的重心,
的重心, 为
为 的中点,
的中点, 在
在 上,且
上,且 ;
;
(1)求证: ;
;
(2)当
 二面角
二面角 的正切值为多少时,
的正切值为多少时, 平面
平面 ;
;
(3)在(2)的条件下,求直线 与平面
与平面 所
所 成角
成角
的正弦值;
已知数列 中,
中, ,且当
,且当 时,函数
时,函数
取得极值;
(Ⅰ)若 ,证明数列
,证明数列 为等差数列;
为等差数列;
(Ⅱ)设数列
 的前
的前 项和为
项和为 ,求
,求  .
.
已知斜三棱柱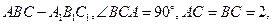
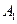 在底面
在底面 上的射影恰为
上的射影恰为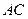 的中点
的中点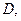 又知
又知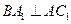 ;
;
(1)求证 :
: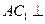 平面
平面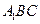 ;
;
(2)求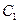 到平面
到平面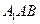 的距离;
的距离;
(3)求二面角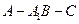 的余弦值;
的余弦值;