．经过天文望远镜的长期观测，人们在宇宙中已经发现了许多双星系统，通过对它们的研究，使我们对宇宙中的物质的存在形式和分布情况有了较深刻的认识。双星系统是由两个星体组成，其中每个星
体的线度都远小于两个星体之间的距离。一般双星系统距离其他星体很远，可以当作孤立系统处理。现根据对某一双星系统的光学测量确定，该双星系统中每个星体的质量都是M，两者间距L，它们正围绕着两者连线的中点作圆周运动。
（1）试计算该双星系统的周期T；
（2）若实验上观测到的运动周期为T’，为了解释两者的不同，目前有一种流行的理论认为，在宇宙中可能存在一种望远镜观测不到的暗物质。作为一种简化模型，我们我们假定在以两个星体连线为直径的球体内均匀分布着密度为ρ的暗物质，而不考虑其它
暗物质的影响，并假设暗物质与星体间的相互作用同样遵守万有引力定律。试根据这一模型计算双星系统的运动周期T’。
正方形的导线框，质量m=60g,边长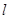
=12cm,电阻R=0.06Ω，在竖直平面内自由下落H=5m后，下边框进入水平方向的匀强磁场中，磁场方向与线框垂直，如图所示，匀强磁场沿竖直方向的宽度h=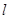,线框通过匀强磁场区域时恰好匀速直线运动。 不计空气阻力，取g=10m/s2。求：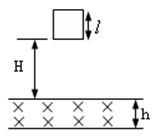
（1）匀强磁场的磁感强度多大？
（2）线框通过磁场区域过程中产生了多少热量？
如图所示，Q为固定的正点电荷，A、B两点在Q的正上方且和Q相距分别为h和0.25h，将一带电量为q的小球（可视为点电荷）从A点由静止释放，运动到B点时速度正好变为零.若此带电小球q在A点处的加速度大小为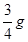
. 试求：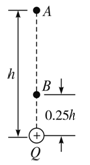
（1）带电小球在B点处的加速度.
（2）A、B两点间的电势差（用Q和h表示）.
如图所示，光滑水平面AB与竖直面内的半圆形导轨在B点平滑相接，导轨半径为R．一个质量为m的物体将弹簧压缩至A点后由静止释放，在弹力作用下物体获得某一向右速度后脱离弹簧，脱离弹簧后当它经过B点进入导轨瞬间对导轨的压力为其重力的9倍，之后向上运动完成半个圆周运动恰好到达C点．已知重力加速度为g．试求：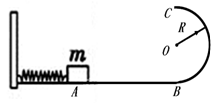
（1）弹簧开始时的弹性势能；
（2）物体从B点运动至C点克服阻力做的功；
（3）物体离开C点后落回水平面时速度的大小．
天文观测到某行星有一颗以半径r、周期
环绕该行星做匀速圆周运动的卫星，已知卫星质量为
，该行星的半径是卫星运动轨道半径的
．求：
（1）该行星的质量M；
（2）该行星表面处的重力加速度g．
在光滑水平面上静置有质量均为m的木板AB和滑块CD，木板AB上表面粗糙．动摩擦因数为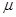
，滑块CD上表面是光滑的1/4圆弧，其始端D点切线水平且在木板AB上表面内，它们紧靠在一起，如图所示．一可视为质点的物块P，质量也为m，从木板AB的右端以初速度v0滑上木板AB，过B点时速度为v0/2，又滑上滑块CD，最终恰好能滑到滑块CD圆弧的最高点C处，求：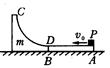
（1）物块滑到B处时木板的速度vAB；
（2）木板的长度L;
（3）滑块CD圆弧的半径R.