在 中,角
中,角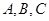 所对应的边分别为
所对应的边分别为 ,且
,且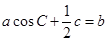
 ,
,
(1)求角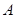 的大小
的大小
(2)若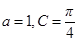 , 求
, 求 的面积
的面积
(1)计算: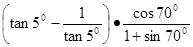
(2)求
 的最大值
的最大值
如图所示,在 中,点
中,点 是
是 的中点,点
的中点,点 在
在 上,且
上,且 ,
, 与
与 交于点
交于点 ,求
,求 与
与 的值。
的值。
设△ABC的内角A,B,C所对的边长分别为a,b,c,且 .
.
(1)求角 的大小;
的大小;
(2)若角 ,
, 边上的中线
边上的中线 的长为
的长为 ,求
,求 的面积.
的面积.
某市去年11份曾发生流感,据统计,11月1日该市新的流感病毒感染者有20人,此后,每天的新感染者平均比前一天的新感染者增加50人,由于该市医疗部门采取措施,使该种病毒的传播得到控制,从某天起,每天的新感染者平均比前一天的新感染者减少30人,到11月30日止,该市在这30日内感染该病毒的患者总共8670人,问11月几日,该市感染此病毒的新患者人数最多?并求这一天的新患者人数.
在直角坐标系中,A (3,0),B (0,3),C
(1)若 ^
^ ,求
,求 的值;
的值;
(2) 与
与 能否共线?说明理由。
能否共线?说明理由。