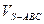(本小题12分)已知抛物线 ,焦点为
,焦点为 ,顶点为
,顶点为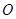 ,点
,点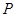 在抛物线上移动,
在抛物线上移动, 是
是 的中点。
的中点。
(1)求点 的轨迹方程;
的轨迹方程;
(2)若倾斜角为60°且过点 的直线交
的直线交 的轨迹于
的轨迹于 两点,求弦长
两点,求弦长 。
。
解下列不等式(组).
1) 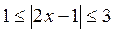 2)
2) 
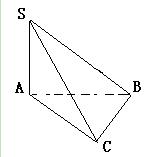
在四棱锥P-ABCD中,底面ABCD是正方形,PD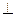 底面ABCD,M,N分别PA,BC的中点,且PD="AD=1" (12分)
底面ABCD,M,N分别PA,BC的中点,且PD="AD=1" (12分)
(1)求证:MN∥平面PCD
(2)求证:平面PAC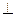 平面PBD
平面PBD
(3)求MN与底面ABCD所成角的大小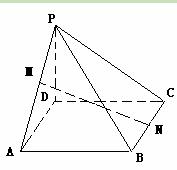
.已知两条直线 :
: ,分别由下列条件确定
,分别由下列条件确定 值
值
①  与
与 相交于点
相交于点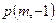
②  ∥
∥
③ 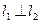 ,且
,且
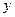 上轴截距为-1
上轴截距为-1
已知函数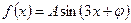 (A>0,0<
(A>0,0<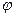 <π)在
<π)在 时取最大值4
时取最大值4
(1)求 的最小正周期
的最小正周期
(2)求 的解析式
的解析式
(3)把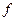
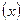 的图像按向量
的图像按向量 平移后得函数
平移后得函数 的图像,求函数
的图像,求函数 的解析式
的解析式
.
在三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=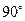 ,且AC=BC=5,SB=
,且AC=BC=5,SB= ,如图
,如图
(1)求侧面sBC与底面ABC所成二面角的大小
(2)求三棱锥的体积