(本小题12分)如图,已知椭圆
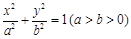 的长轴为
的长轴为 ,过点
,过点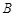 的直线
的直线 与
与 轴垂直.直线
轴垂直.直线 所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率
所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率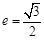 。
。
(1)求椭圆的标准方程;
(2)设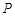 是椭圆上异于
是椭圆上异于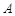 、
、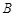 的任意一点,
的任意一点,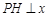 轴,
轴,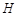 为垂足,延长
为垂足,延长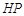 到点
到点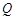 使得
使得 ,连结
,连结 延长交直线
延长交直线 于点
于点 ,
,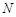 为
为 的中点.试判断直线
的中点.试判断直线 与以
与以 为直径的圆
为直径的圆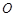 的位置关系。
的位置关系。
在直角坐标系 xOy中,曲线 C的参数方程为 ,(θ为参数),直线 l的参数方程为 ,( t为参数).
(1)若 a=﹣1,求 C与 l的交点坐标;
(2)若 C上的点到 l距离的最大值为 ,求 a.
已知函数 f( x)= e x( e x﹣ a)﹣ a 2 x.
(1)讨论 f( x)的单调性;
(2)若 f( x)≥0,求 a的取值范围.
设 A, B为曲线 C: y 上两点, A与 B的横坐标之和为4.
(1)求直线 AB的斜率;
(2)设 M为曲线 C上一点, C在 M处的切线与直线 AB平行,且 AM⊥ BM,求直线 AB的方程.
为了监控某种零件的一条生产线的生产过程,检验员每隔30 min从该生产线上随机抽取一个零件,并测量其尺寸(单位: cm).下面是检验员在一天内依次抽取的16个零件的尺寸:
|
抽取次序 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
零件尺寸 |
9.95 |
10.12 |
9.96 |
9.96 |
10.01 |
9.92 |
9.98 |
10.04 |
|
抽取次序 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
零件尺寸 |
10.26 |
9.91 |
10.13 |
10.02 |
9.22 |
10.04 |
10.05 |
9.95 |
经计算得 x i=9.97, s 0.212, 18.439, ( x i )( i﹣8.5)=﹣2.78,其中 x i为抽取的第 i个零件的尺寸, i=1,2,…,16.
(1)求( x i, i)( i=1,2,…,16)的相关系数 r,并回答是否可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小(若| r|<0.25,则可以认为零件的尺寸不随生产过程的进行而系统地变大或变小).
(2)一天内抽检零件中,如果出现了尺寸在( 3 s, 3 s)之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
(ⅰ)从这一天抽检的结果看,是否需对当天的生产过程进行检查?
(ⅱ)在( 3 s, 3 s)之外的数据称为离群值,试剔除离群值,估计这条生产线当天生产的零件尺寸的均值与标准差.(精确到0.01)
附:样本( x i, y i)( i=1,2,…, n)的相关系数 r , 0.09.
如图,在四棱锥 P﹣ ABCD中, AB∥ CD,且∠ BAP=∠ CDP=90°.
(1)证明:平面 PAB⊥平面 PAD;
(2)若 PA= PD= AB= DC,∠ APD=90°,且四棱锥 P﹣ ABCD的体积为 ,求该四棱锥的侧面积.
