(本小题满分12分)
已知f(x)=sin(2x+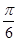 )+sin(2x-
)+sin(2x-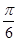 )+2cos2x+a,当x∈[-
)+2cos2x+a,当x∈[- ,
, ]时,f(x)的最小值为-3,求α的值.
]时,f(x)的最小值为-3,求α的值.
(本小题满分12分)
已知向量 =(3,-4),
=(3,-4), =(6,-3),
=(6,-3),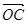 =(5-m,-(3+m)).
=(5-m,-(3+m)).
(1)若点A、B、C能构成三角形,求实数m应满足的条件;
(2)若△ABC为直角三角形,且∠A为直角,求实数m的值.
(本小题满分10分)
已知cosα= ,且-
,且- <α<0,
<α<0,
求 的值.
的值.
(本小题满分10分)
.设数列 的前项n和为
的前项n和为 ,若对于任意的正整数n都有
,若对于任意的正整数n都有 .
.
(1)设 ,求证:数列
,求证:数列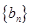 是等比数列,并求出
是等比数列,并求出 的通项公式。
的通项公式。
(2)求数列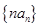 的前n项和.
的前n项和.
(文)已知 在
在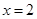 处有极值,其图象在
处有极值,其图象在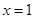 处的切线与直线
处的切线与直线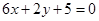 平行.
平行.
(1)求函数的单调区间;
(2)若 时,
时,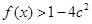 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。