(本小题满分10分)
.设数列 的前项n和为
的前项n和为 ,若对于任意的正整数n都有
,若对于任意的正整数n都有 .
.
(1)设 ,求证:数列
,求证:数列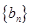 是等比数列,并求出
是等比数列,并求出 的通项公式。
的通项公式。
(2)求数列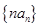 的前n项和.
的前n项和.
已知椭圆 的左右焦点
的左右焦点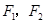 ,其离心率为
,其离心率为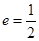 ,点
,点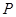 为椭圆上的一个动点,
为椭圆上的一个动点,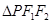 内切圆面积的最大值为
内切圆面积的最大值为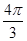 .
.
(1)求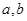 的值;
的值;
(2)若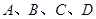 是椭圆上不重合的四个点,且满足
是椭圆上不重合的四个点,且满足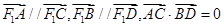 ,求
,求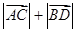 的取值范围.
的取值范围.
如图,已知四棱锥P-ABCD,底面ABCD为边长为2的菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.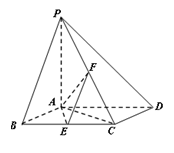
(Ⅰ)判定AE与PD是否垂直,并说明理由;
(Ⅱ)若PA=2,求二面角E-AF-C的余弦值.
某工厂为了检查一条流水线的生产情况,从该流水线上随机抽取40件产品,测量这些产品的重量(单位:克),整理后得到如下的频率分布直方图(其中重量的分组区间分别为(490,495],(495,500],(500,505],(505,510],(510,515])
(1)若从这40件产品中任取两件,设X为重量超过505克 的产品数量,求随机变量X的分布列;
(2)若将该群体分别近似看作总体分布,现从该流水线上任取5件产品,求恰有两件产品的重量超过505克的概率.
已知数列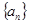 前n项和为
前n项和为 ,满足
,满足
(1)证明: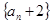 是等比数列,并求
是等比数列,并求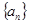 的通项公式;
的通项公式;
(2)数列 满足
满足 ,
, 为数列
为数列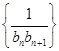 的前n项和,若
的前n项和,若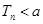 对正实数a都成立,求a的取值范围.
对正实数a都成立,求a的取值范围.
设函数 ,
, .
.
(1)当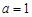 时,求不等式
时,求不等式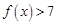 的解集;
的解集;
(2)对任意 ,
, 恒有
恒有 ,求实数
,求实数 的取值范围.
的取值范围.