如图,已知四棱锥P-ABCD,底面ABCD为边长为2的菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.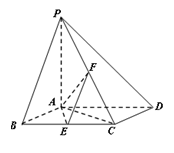
(Ⅰ)判定AE与PD是否垂直,并说明理由;
(Ⅱ)若PA=2,求二面角E-AF-C的余弦值.
已知矩阵A= 属于特征值l的一个特征向量为α=
属于特征值l的一个特征向量为α= .
.
(1)求实数b,l的值;
(2)若曲线C在矩阵A对应的变换作用下,得到的曲线为C¢:x2+2y2=2,求曲线C的方程.
如图,PA是圆O的切线,A为切点,PO与圆O交于点B、C,AQ^OP,垂足为Q.若PA=4,PC=2,求AQ的长.
已知函数f(x)=ax3+|x-a|,a R.
R.
(1)若a=-1,求函数y=f(x) (x [0,+∞))的图象在x=1处的切线方程;
[0,+∞))的图象在x=1处的切线方程;
(2)若g(x)=x4,试讨论方程f(x)=g(x)的实数解的个数;
(3)当a>0时,若对于任意的x1 [a,a+2],都存在x2
[a,a+2],都存在x2 [a+2,+∞),使得f(x1)f(x2)=1024,求满足条件的正整数a的取值的集合.
[a+2,+∞),使得f(x1)f(x2)=1024,求满足条件的正整数a的取值的集合.
如图(示意),公路AM、AN围成的是一块顶角为α的角形耕地,其中tanα=-2.在该块土地中P处有一小型建筑,经测量,它到公路AM,AN的距离分别为3km,km.现要过点P修建一条直线公路BC,将三条公路围成的区域ABC建成一个工业园.为尽量减少耕地占用,问如何确定B点的位置,使得该工业园区的面积最小?并求最小面积.
给定椭圆C: (a>b>0),称圆C1:x2+y2=a2+b2为椭圆C的“伴随圆”.已知椭圆C的离心率为
(a>b>0),称圆C1:x2+y2=a2+b2为椭圆C的“伴随圆”.已知椭圆C的离心率为 ,且经过点(0,1).
,且经过点(0,1).
(1)求实数a,b的值;
(2)若过点P(0,m)(m>0)的直线l与椭圆C有且只有一个公共点,且l被椭圆C的伴随圆C1所截得的弦长为2 ,求实数m的值.
,求实数m的值.