选修4—1 几何证明选讲
已知△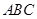 内接于⊙
内接于⊙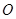 ,
,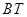 为⊙
为⊙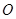 的切线,
的切线,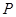 为直线
为直线 上一点,过点
上一点,过点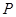 作
作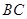 的平行线交直线
的平行线交直线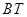 于点
于点 ,交直线
,交直线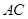 于点
于点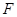 .
.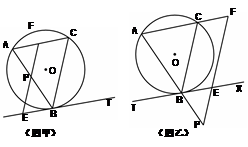
(Ⅰ)如图甲,求证:当点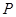 在线段
在线段 上时,
上时,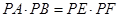 ;
;
(Ⅱ)如图乙,当点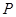 在线段
在线段 的延长线上时,(Ⅰ)的结论是否仍成立?如果成立,请给予证明;如果不成立,请说明理由.
的延长线上时,(Ⅰ)的结论是否仍成立?如果成立,请给予证明;如果不成立,请说明理由.
(理)设进入某商场的每一位顾客购买甲种商品的概率为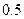 ,购买乙种商品的概率为
,购买乙种商品的概率为 ,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的。
,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的。
(Ⅰ)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(Ⅱ)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率;
(Ⅲ)记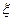 表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求
表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求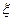 的分布列及期望。
的分布列及期望。
(文)已知向量m=(sinA,cosA),n=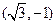 ,m·n=1,且A为锐角.
,m·n=1,且A为锐角.
(Ⅰ)求角A的大小;(Ⅱ)求函数 的值域.
的值域.
(理)已知向量m=(sinA,cosA),n= ,m·n=1,且A为锐角.
,m·n=1,且A为锐角.
(Ⅰ)求角A的大小;(Ⅱ)求函数 的值域.
的值域.
(文)等差数列 中,
中, 且
且 成等比数列,求数列
成等比数列,求数列 前20项的和
前20项的和 .
.
已知抛物线 的焦点为F,以点
的焦点为F,以点 为圆心,|AF|为半径的圆在x轴的上方与抛物线交于M、N两点。
为圆心,|AF|为半径的圆在x轴的上方与抛物线交于M、N两点。
(I)求证:点A在以M、N为焦点,且过点F的椭圆上;
(II)设点P为MN的中点,是否存在这样的a,使得|FP|是|FM|与|FN|的等差中项?如果存在,求出实数a的值;如果不存在,请说明理由。