某化工厂引进一条先进生产线生产某种化工产品,其生产的总成本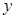 (万元)与年产量
(万元)与年产量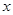 (吨)之间的函数关系式可以近似地表示为
(吨)之间的函数关系式可以近似地表示为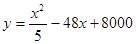 ,已知此生产线年产量最大为210吨。
,已知此生产线年产量最大为210吨。
(1)求年产量为多少吨时,生产每吨产品的平均成本最低,并求每吨产品平均最低成本;
(2)若每吨产品平均出厂价为40万元,那么当年产量为多少吨时,可以获得最大利润?最大利润是多少?
已知直线L:x-2y-5=0与圆C:x2+y2=50.求:
(1)交点A,B的坐标;(2)△AOB的面积
求圆心在直线3x+y-5=0上,并且经过原点和点(4,0)的圆的方程
已知正项数列 在抛物线
在抛物线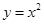 上;数列
上;数列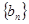 中,点
中,点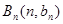 在过点(0,1),以
在过点(0,1),以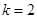 为斜率的直线上。
为斜率的直线上。
(1)求数列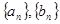 的通项公式;
的通项公式;
(2)若 成立,若存在,求出k值;若不存在,请说明理由;
成立,若存在,求出k值;若不存在,请说明理由;
(3)对任意正整数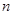 ,不等式
,不等式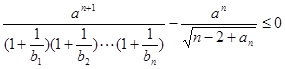 恒成立,求正数
恒成立,求正数 的取值范围。
的取值范围。
作为绍兴市2013年5.1劳动节系列活动之一的花卉展在镜湖湿地公园举行.现有一占地1800平方米的矩形地块,中间三个矩形设计为花圃(如图),种植有不同品种的观赏花卉,周围则均是宽为1米的赏花小径,设花圃占地面积为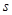 平方米,矩形一边的长为
平方米,矩形一边的长为 米(如图所示)
米(如图所示)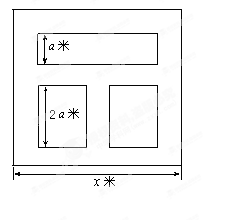
(1)试将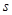 表示为
表示为 的函数;
的函数;
(2)问应该如何设计矩形地块的边长,使花圃占地面积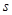 取得最大值.
取得最大值.
在等比数列 中,已知
中,已知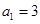 ,公比
,公比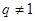 ,等差数列
,等差数列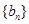 满足
满足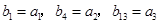 .
.
(Ⅰ)求数列 与
与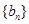 的通项公式;
的通项公式;
(Ⅱ)记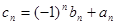 ,求数列
,求数列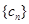 的前n项和
的前n项和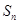 .
.