已知正项数列 在抛物线
在抛物线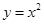 上;数列
上;数列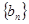 中,点
中,点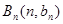 在过点(0,1),以
在过点(0,1),以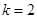 为斜率的直线上。
为斜率的直线上。
(1)求数列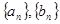 的通项公式;
的通项公式;
(2)若 成立,若存在,求出k值;若不存在,请说明理由;
成立,若存在,求出k值;若不存在,请说明理由;
(3)对任意正整数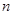 ,不等式
,不等式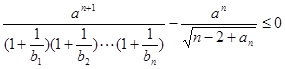 恒成立,求正数
恒成立,求正数 的取值范围。
的取值范围。
设数列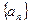 的前
的前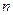 项和为
项和为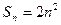 ,数列
,数列 为等比数列,且
为等比数列,且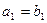 ,
,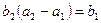 。(1)求数列
。(1)求数列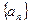 和
和 的通项公式;(2)设
的通项公式;(2)设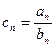 ,求数列
,求数列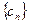 的前
的前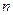 项和
项和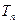 。
。
如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量。已知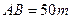 ,
, ,于
,于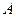 处测得水深
处测得水深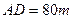 ,于
,于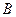 处测得水深
处测得水深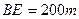 ,于
,于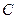 处测得水深
处测得水深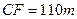 ,求
,求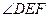 的余弦值。
的余弦值。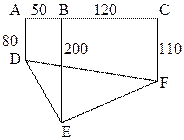
围建一个面积为360 的矩形场地,要求矩形场地的一面利用旧墙(利用的旧墙需维修),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽度为2
的矩形场地,要求矩形场地的一面利用旧墙(利用的旧墙需维修),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽度为2 的进出口,如图所示。已知旧墙的维修费用为45元/
的进出口,如图所示。已知旧墙的维修费用为45元/ ,新墙的造价为180元/
,新墙的造价为180元/ 。设利用的旧墙长度为
。设利用的旧墙长度为 (单位:
(单位: ),修建此矩形场地围墙的总费用为
),修建此矩形场地围墙的总费用为 (单位:元) (Ⅰ)将
(单位:元) (Ⅰ)将 表示为
表示为 的函数;(Ⅱ)试确定
的函数;(Ⅱ)试确定 ,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
在各项均为负数的数列 中,已知
中,已知 ,且
,且 ,(1)求证:数列
,(1)求证:数列 是等比数列,并求出通项公式。
是等比数列,并求出通项公式。
(2)试问 是否为该数列的项?若是,是第几项?若不是,请说明理由。
是否为该数列的项?若是,是第几项?若不是,请说明理由。
在锐角三角形ABC中, 、
、 、
、 分别为角A、B、C 所对的边,且
分别为角A、B、C 所对的边,且
 。(Ⅰ)确定角C的大小;(Ⅱ)若
。(Ⅰ)确定角C的大小;(Ⅱ)若 且△ABC的面积为
且△ABC的面积为 ,求
,求 的值。
的值。