设数列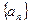 的前
的前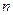 项和为
项和为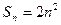 ,数列
,数列 为等比数列,且
为等比数列,且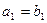 ,
,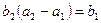 。(1)求数列
。(1)求数列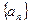 和
和 的通项公式; (2)设
的通项公式; (2)设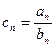 ,求数列
,求数列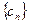 的前
的前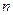 项和
项和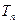 。
。
某服装厂生产一种服装,每件服装的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100件时,每多订购一件,订购的全部服装的出厂单价就降低0.02元. 根据市场调查,销售商一次订购量不会超过500件。
(1)设一次订购量为 件,服装的实际出厂单价为
件,服装的实际出厂单价为 元,写出函数
元,写出函数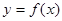 的表达式;
的表达式;
(2)当销售商一次订购了450件服装时,该服装厂获得的利润是多少元?
(服装厂售出一件服装的利润=实际出厂单价-成本)
已知函数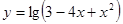 的的定义域为
的的定义域为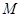 .当
.当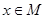 时,求函数
时,求函数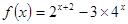 的最值及相应的
的最值及相应的 的值。
的值。
设集合 ,
, 。
。
(1)当 时,求
时,求 的非空真子集的个数;
的非空真子集的个数;
(2)若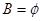 ,求
,求 的取值范围;
的取值范围;
(3)若 ,求
,求 的取值范围。
的取值范围。
设 x1、x2( )是函数
)是函数  (
(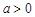 )的两个极值点.
)的两个极值点.
(I)若  ,
,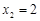 ,求函数
,求函数 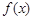 的解析式;
的解析式;
(II)若  ,求 b 的最大值;
,求 b 的最大值;
已知三次函数 的导函数
的导函数 ,
, ,
,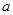 、
、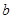 为实数。
为实数。
(Ⅰ)若曲线
 在点(
在点( ,
,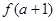 )处切线的斜率为12,求
)处切线的斜率为12,求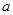 的值;
的值;
(Ⅱ)若 在区间[-1,1]上的最小值、最大值分别为-2、1,且
在区间[-1,1]上的最小值、最大值分别为-2、1,且 ,求函数
,求函数 的解析式。
的解析式。