已知椭圆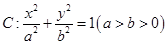 的左、右焦点分别为
的左、右焦点分别为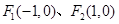 ,且经过定点
,且经过定点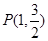 ,
,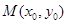 为椭圆
为椭圆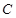 上的动点,以点
上的动点,以点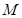 为圆心,
为圆心,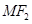 为半径作圆
为半径作圆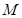 .
.
(1)求椭圆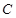 的方程;
的方程;
(2)若圆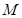 与
与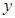 轴有两个不同交点,求点
轴有两个不同交点,求点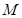 横坐标
横坐标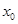 的取值范围;
的取值范围;
(3)是否存在定圆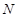 ,使得圆
,使得圆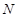 与圆
与圆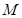 恒相切?若存在,求出定圆
恒相切?若存在,求出定圆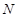 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(本小题满分13分)
设数列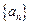 的前
的前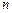 项和为
项和为 ,且满足
,且满足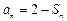
 .
.
(1)求 ,
,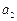 ,
, ,
, 的值并猜想这个数列的通项公式
的值并猜想这个数列的通项公式
(2)证明数列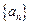 是等比数列.
是等比数列.
(本小题满分12分) 分别是椭圆
分别是椭圆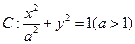 的左右焦点,直线
的左右焦点,直线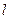 与C相交于A,B两点
与C相交于A,B两点
(1)直线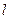 斜率为1且过点
斜率为1且过点 ,若
,若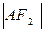 ,
,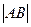 ,
,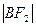 成等差数列,,求
成等差数列,,求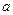 值
值
(2)若直线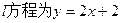 ,且
,且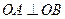 ,求
,求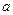 值.
值.
本小题满分12分)
对于任意的实数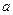 ,不等式
,不等式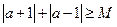 恒成立,记实数
恒成立,记实数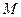 的最大值是
的最大值是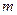 .
.
(1)求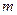 的值;
的值;
(2)解不等式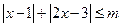 .
.
(本小题满分12分)
已知数列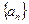 满足
满足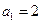 ,且
,且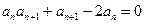 (
(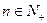 )。
)。
(1)求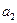 、
、 、
、 的值;
的值;
(2)猜想数列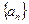 的通项公式,并用数学归纳法加以证明。
的通项公式,并用数学归纳法加以证明。
(本小题满分12分)
已知投资某项目的利润与产品价格的调整有关,在每次调整中价格下降的概率都是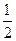 .设该项目产品价格在一年内进行2次独立的调整,记产品价格在一年内的下降次数为
.设该项目产品价格在一年内进行2次独立的调整,记产品价格在一年内的下降次数为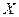 ,对该项目每投资十万元,
,对该项目每投资十万元,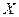 取0、1、2时,一年后相应的利润为1.6万元、2万元、2.4万元.求投资该项目十万元,一年后获得利润的数学期望及方差.
取0、1、2时,一年后相应的利润为1.6万元、2万元、2.4万元.求投资该项目十万元,一年后获得利润的数学期望及方差.