设函数f(x)=loga(ax+ ).(1)判断函数f(x)的奇偶性;
).(1)判断函数f(x)的奇偶性;
(2)判断函数f(x)在(0,+∞)的单调性并证明.
某房建公司在市中心用100万元购买一块土地,计划建造一幢每层为1000平方米的n
层楼房,第一层每平方米所需建筑费用(不包括购买土地费用)为600元,第二层每平
方米所需建筑费用为700元,…,以后每升高一层,每平方米的建筑费用增加100元.
(1)写出每平方米平均造价y(以百元为单位)用n表示的表达式;
(2)为使整个大楼每平方米的平均造价不超过1150元,则这幢大楼最多能造几层?
已知向量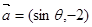 与
与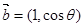 互相垂直,其中
互相垂直,其中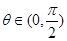 .
.
(1)求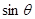 和
和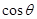 的值;
的值;
(2)若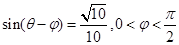 ,求
,求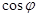 的值.
的值.
已知等差数列{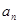 }中,
}中,
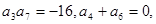 求{
求{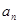 }前n项和
}前n项和 . .
. .
已知椭圆C的离心率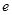 =
=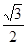 ,长轴的左右两个端点分别为
,长轴的左右两个端点分别为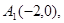
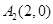 ;
;
(1)求椭圆C的方程;
(2)点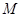 在该椭圆上,且
在该椭圆上,且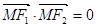 ,求点
,求点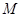 到
到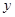 轴的距离;
轴的距离;
(3)过点(1,0)且斜率为1的直线与椭圆交于P,Q两点,求△OPQ的面积.
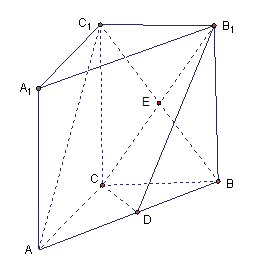
如图, 在直三棱柱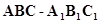 中,
中,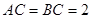 ,
,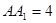 ,
, 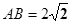 ,点
,点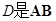 的中点,
的中点,
(I)求证: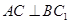
(II)求证: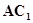 //平面
//平面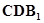 ;
;
(Ⅲ)求几何体 的体积.
的体积.