函数 的定义域为(0,1](
的定义域为(0,1]( 为实数).
为实数).
⑴当 时,求函数
时,求函数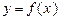 的值域;
的值域;
⑵若函数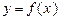 在定义域上是减函数,求
在定义域上是减函数,求 的取值范围;
的取值范围;
⑶求函数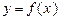 在x∈(0,1]上的最大值及最小值,并求出函数取最值时
在x∈(0,1]上的最大值及最小值,并求出函数取最值时 的值.
的值.
设P,Q,R,S四人分比获得1——4等奖,已知:
(1)若P得一等奖,则Q得四等奖;
(2)若Q得三等奖,则P得四等奖;
(3)P所得奖的等级高于R;
(4)若S未得一等奖,则P得二等奖;
(5)若Q得二等奖,则R不是四等奖;
(6)若Q得一等奖,则R得二等奖。
问P,Q,R,S分别获得几等奖?
写出下列各命题的否命题和命题的否定:
(1) ,若
,若 ,则
,则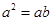 ;
;
(2)若 ,则
,则 ;
;
(3)若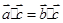 ,则
,则 ;
;
(4)若 ,则
,则 是等比数列。
是等比数列。
写出命题“所有等比数列 的前
的前 项和是
项和是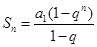 (
(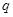 是公比)”的否定,并判断原命题否定的真假。
是公比)”的否定,并判断原命题否定的真假。
判断下列命题的真假,并说明理由:
(1)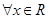 ,都有
,都有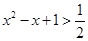 ;
;
(2)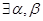 ,使
,使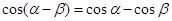 ;
;
(3)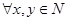 ,都有
,都有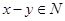 ;
;
(4)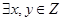 ,使
,使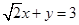 。
。
设命题为“若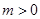 ,则关于
,则关于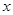 的方程
的方程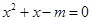 有实数根”,试写出它的否命题、逆命题和逆否命题,并分别判断它们的真假.
有实数根”,试写出它的否命题、逆命题和逆否命题,并分别判断它们的真假.