为了让学生了解更多“奥运会”知识,某中学举行了一次“奥运知识竞赛”,共有800名学生参加了这次竞赛,为了解本次竞赛成绩情况,从中抽取部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表,解答下列问题:
(1)若用系统抽样的方法抽取50个样本,现将所有学生随机地编号为000,001,002,…,799,试写出第二组第一位学生的编号;
(2)填充频率分布表的空格(将答案直接填在表格内),并作出频率分布直方图;
(3)若成绩在85.5~95.5分的学生为二等奖,问参赛学生中获得二等奖的学生约为多少人?
(本小题满分10分)某车间生产一种仪器的固定成本是10000元,每生产一台该仪器需要增加投入100元,已知总收益满足函数: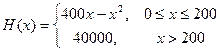 ,其中
,其中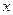 是仪器的月产量。
是仪器的月产量。
(1)将利润表示为月产量的函数(用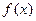 表示);
表示);
(2)当月产量为何值时,车间所获利润最大?最大利润是多少元?(总收益=总成本+利润)
(本小题满分9分)以下是用二分法求方程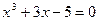 的一个近似解(精确度为0.1)的不完整的过程,请补充完整。
的一个近似解(精确度为0.1)的不完整的过程,请补充完整。
| 区间 |
中点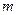 |
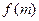 符号 符号 |
区间长度 |
解:设函数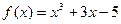 ,其图象在
,其图象在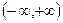 上是连续不断的,且
上是连续不断的,且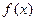 在
在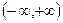 上是单调递______(增或减)。先求
上是单调递______(增或减)。先求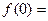 _______,
_______,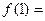 ______,
______,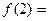 ____________。
____________。
所以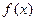 在区间____________内存在零点
在区间____________内存在零点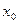 ,再填上表:
,再填上表:
下结论:_______________________________。
(可参考条件: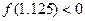 ,
,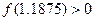 ;符号填+、-)
;符号填+、-)
(本小题满分9分)已知R为全集,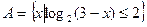 ,
,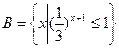 ,求(
,求( RA)
RA)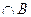
设有一张边长为48cm的正方形铁皮 ,从其四个角各截去一个大小相同的小正方形 ,然后将剩余部分折成一个无盖的长方体盒子 ,所得盒子的体积V是关于截去的小正方形的边长x的函数 .
(1)随着x的变化 ,盒子体积V是如何变化的?
(2)截去的小正方形的边长x为多少时 ,盒子的体积最大?最大体积是多少?
已知曲线y = 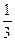
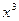 +
+ 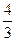 .
.
(1)求曲线在点A(2 ,4)处的切线方程 ;
(2)求曲线的切线与坐标轴围成的三角形的面积 .