已知关于x的方程:x2﹣(6+i)x+9+ai=0(a∈R)有实数根b.
(1)求实数a,b的值.
(2)若复数z满足| ﹣a﹣bi|﹣2|z|=0,求z为何值时,|z|有最小值,并求出|z|的值.
﹣a﹣bi|﹣2|z|=0,求z为何值时,|z|有最小值,并求出|z|的值.
某工厂每天生产某种产品最多不超过40件,并且在生产过程中产品的正品率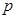 与每日生产产品件数
与每日生产产品件数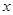 (
(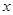
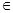
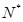 )间的关系为
)间的关系为 ,每生产一件正品盈利4000元,每出现一件次品亏损2000元.
,每生产一件正品盈利4000元,每出现一件次品亏损2000元.
(注:正品率=产品的正品件数÷产品总件数×100%)
(1)将日利润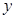 (元)表示成日产量
(元)表示成日产量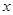 (件)的函数;
(件)的函数;
(2)求该厂的日产量为多少件时,日利润最大?并求出日利润的最大值.
设函数 =
= (
(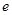 为自然对数的底数),
为自然对数的底数), ,记
,记 .
.
(1) 为
为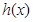 的导函数,判断函数
的导函数,判断函数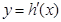 的单调性,并加以证明;
的单调性,并加以证明;
(2)若函数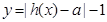 =0有两个零点,求实数
=0有两个零点,求实数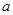 的取值范围.
的取值范围.
已知数列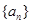 为递减的等差数列,
为递减的等差数列, 是数列
是数列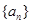 的前
的前 项和,且
项和,且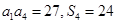 .
.
⑴ 求数列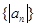 的前
的前 项和
项和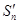
⑵ 令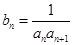 ,求数列
,求数列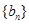 的前
的前 项和
项和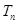
在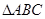 中,角
中,角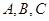 所对的边分别为
所对的边分别为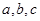 ,且满足
,且满足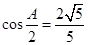 ,
,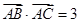
(1)求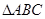 的面积;(2)若
的面积;(2)若 ,求
,求 的值.
的值.
(本小题满分13分)已知函数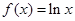 ,
, .
.
(Ⅰ)设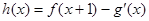 (其中
(其中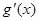 是
是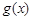 的导函数),求
的导函数),求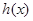 的最大值;
的最大值;
(Ⅱ)求证: 当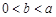 时,有
时,有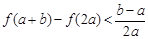 ;
;
(Ⅲ)设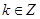 ,当
,当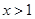 时,不等式
时,不等式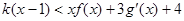 恒成立,求
恒成立,求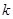 的最大值.
的最大值.