设函数
=
（
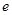为自然对数的底数），
，记
．
（1）
为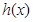
的导函数，判断函数
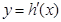的单调性，并加以证明；
（2）若函数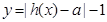
=0有两个零点，求实数
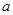的取值范围．
(2)长为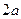
的线段两端点分别在直角坐标轴上移动，从原点向该线段作垂线，垂足为
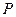，求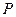的轨迹的极坐标方程.
如图所示，
为⊙
的直径，
、
为⊙的切线，
、
为切点
(1)求证：
(2)若⊙的半径为
，求AD·OC的值.
线段
过
轴正半轴上一定点
，两端点
、
到轴的距离之积为
，
为坐标原点，以轴为对称轴，经过、、三点作抛物线.
（1）求这条抛物线方程；
（2）若
求
的最大值.
已知点
)都在函数
的图象上.
(1)若数列
是等差数列,求证数列
为等比数列；
(2)若数列的前
项和为
=
,过点
的直线与两坐标轴所围成三角形面积为
,求使
对
恒成立的实数
的取值范围.
已知函数
，函数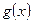
的图像与函数
的图像关于直线
对称.
（1）求函数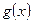的解析式；
（2）若函数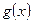在区间
上的值域为
，
求实数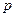
的取值范围；
（3）设函数
，试用列举法表示集合
.