(本小题满分14分)
设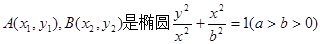 上的两点,
上的两点,
满足 ,椭圆的离心率
,椭圆的离心率 短轴长为2,0为坐标原点.
短轴长为2,0为坐标原点.
(1)求椭圆的方程;
(2)试问:△AOB的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
(本小题满分14分)
已知函数 在
在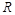 上有定义,对任意实数
上有定义,对任意实数 和任意实数
和任意实数 ,都有
,都有 .
.
(Ⅰ)证明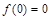 ;
;
(Ⅱ)证明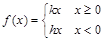 (其中k和h均为常数);
(其中k和h均为常数);
(Ⅲ)当(Ⅱ)中 的时,设
的时,设 ,讨论
,讨论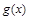 在
在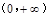 内的单调性.
内的单调性.
(本小题满分12分)
如图,在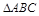 中,设
中,设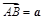 ,
, ,
, 的中点为
的中点为 ,
, 的中点为
的中点为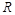 ,
, 的中点恰为
的中点恰为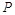 .
.
(Ⅰ)若 ,求
,求 和
和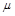 的值;
的值;
(Ⅱ)以 ,
,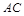 为邻边,
为邻边,  为对角线,作平行四边形
为对角线,作平行四边形 ,
,
求平行四边形 和三角形
和三角形 的面积之比
的面积之比 .
.
(本小题满分12分)
已知 的内角
的内角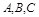 所对的边分别是
所对的边分别是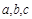 ,设向量
,设向量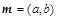 ,
,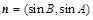 ,
, .
.
(Ⅰ)若 //
// ,求证:
,求证: 为等腰三角形;
为等腰三角形;
(Ⅱ)若 ⊥
⊥ ,边长
,边长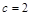 ,
, ,求
,求 的面积.
的面积.
(本小题满分13分)
已知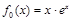 ,
,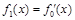 ,
,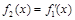 ,…,
,…,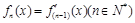 .
.
(Ⅰ)请写出的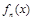 表达式(不需证明);
表达式(不需证明);
(Ⅱ)求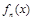 的极小值
的极小值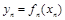 ;
;
(Ⅲ)设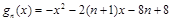 ,
,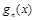 的最大值为
的最大值为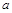 ,
,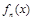 的最小值为
的最小值为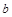 ,试求
,试求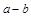 的最小值.
的最小值.
(本小题满分12分)
已知命题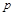 :实数
:实数 满足
满足 ;命题
;命题 :实数
:实数 满足
满足 ,若
,若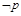 是
是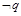 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围.
的取值范围.