（本小题满分13分）
已知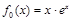
，
，
，…，
.
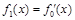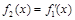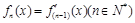（Ⅰ）请写出的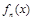
表达式（不需证明）；
（Ⅱ）求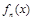的极小值
；
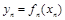（Ⅲ）设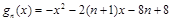
，
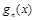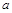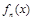的最大值为
，的最小值为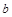
，试求
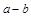的最小值.
如图所示，正方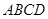形
与直角梯形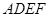
所在平面互相垂直，
，
，
.
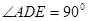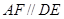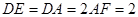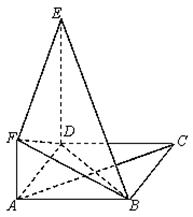
(1)求证：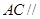
平面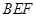
；
(2)求四面体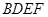
的体积.
某工厂某种产品的年固定成本为250万元，每生产
千件，需另投入成本为
，当年产量不足80千件时，
（万元）.当年产量不小于80千件时，
（万元）.每件商品售价为0.05万元.通过市场分析，该厂生产的商品能全部售完.
(1)写出年利润
（万元）关于年产量（千件）的函数解析式；
(2)年产量为多少千件时，该厂在这一商品的生产中所获利润最大？
设p:函数
的定义域为R; q:不等式
,对
∈(-∞,-1)上恒成立,如果命题“p∨q”为真命题,命题“p∧q”为假命题,求实数
的取值范围.
已知
在区间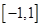
上是增函数.
（1）求实数
的值组成的集合
；
（2）设关于
的方程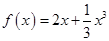
的两个非零实根为
、
．试问：是否存在实数
，使得不等式
对任意
及
恒成立？若存在，求的取值范围；若不存在，请说明理由.
已知椭圆
，
、
是其左右焦点，离心率为
，且经过点
.
（1）求椭圆
的标准方程；
（2）若
、
分别是椭圆长轴的左右端点，
为椭圆上动点，设直线
斜率为
，且
，求直线
斜率的取值范围；
（3）若为椭圆上动点，求
的最小值.