高三年级有3名男生和1名女生为了报某所大学,事先进行了多方详细咨询,并根据自己的高考成绩情况,最终估计这3名男生报此所大学的概率都是 ,这1名女生报此所大学的概率是
,这1名女生报此所大学的概率是 .且这4人报此所大学互不影响。
.且这4人报此所大学互不影响。
(Ⅰ)求上述4名学生中报这所大学的人数中男生和女生人数相等的概率;
(Ⅱ)在报考某所大学的上述4名学生中,记 为报这所大学的男生和女生人数的和,试求
为报这所大学的男生和女生人数的和,试求 的分布列和数学期望.
的分布列和数学期望.
(本题满分14分)
已知数列 的前
的前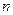 项和为
项和为 ,点
,点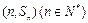 均在
均在 函数
函数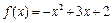 的图象上
的图象上
(1)求数列 的通项公式
的通项公式
(2)若数列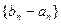 的首项是1,公比为
的首项是1,公比为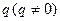 的等比数列,求数列
的等比数列,求数列 的前
的前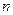 项和
项和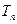
( 本题满分15分)
本题满分15分)
已知偶函 数
数 满足:当
满足:当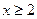 时,
时,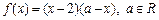 ,当
,当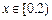 时,
时,
(1) 求当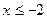 时,
时,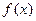 的表达式;
的表达式;
(2) 若直线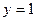 与函数
与函数 的图象恰好有两个公共点,求实数
的图象恰好有两个公共点,求实数 的取值范围。
的取值范围。 (3) 试讨论当实数
(3) 试讨论当实数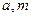 满足什么条件时,函数
满足什么条件时,函数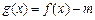 有4个零点且这4个零点从小到大依次成等差数列。
有4个零点且这4个零点从小到大依次成等差数列。
(本题满分15分)已知函数
(1) 求函数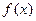 的最小值
的最小值
(2)求证:当 时
时 ,
,
(本题满分14分)
已知函数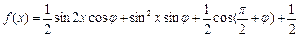 ,
,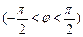 ,其图象过点
,其图象过点
(1) 求 的解析式,并求对称中心
的解析式,并求对称中心
(2) 将函数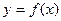 的图象上各点纵坐标不变,横坐标扩大为原来的2倍,然后各点横坐标不变,纵坐标扩大为原来的2倍,得到
的图象上各点纵坐标不变,横坐标扩大为原来的2倍,然后各点横坐标不变,纵坐标扩大为原来的2倍,得到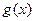 的图象,求函数
的图象,求函数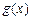 在
在 上的最大值和最小值.
上的最大值和最小值.
(本小题满分12分)
设双曲线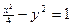 的右顶点为
的右顶点为 是双曲线上异于顶点的一个动点,从
是双曲线上异于顶点的一个动点,从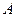 引双曲线的两条渐近线的平行线与直线
引双曲线的两条渐近线的平行线与直线 (
( 为坐标原点)分别交于
为坐标原点)分别交于 和
和 两点.
两点.
(1) 证明:无论 点在什么位置,总有
点在什么位置,总有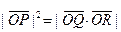 ;
;
(2) 设动点 满足条件:
满足条件:  , 求点
, 求点 的轨迹方程.
的轨迹方程.