(本小题满分12分)
设双曲线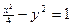 的右顶点为
的右顶点为 是双曲线上异于顶点的一个动点,从
是双曲线上异于顶点的一个动点,从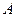 引双曲线的两条渐近线的平行线与直线
引双曲线的两条渐近线的平行线与直线 (
( 为坐标原点)分别交于
为坐标原点)分别交于 和
和 两点.
两点.
(1) 证明:无论 点在什么位置,总有
点在什么位置,总有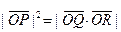 ;
;
(2) 设动点 满足条件:
满足条件:  , 求点
, 求点 的轨迹方程.
的轨迹方程.
已知数列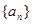 是各项均为正数的等差数列,首项
是各项均为正数的等差数列,首项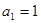 ,其前
,其前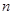 项和为
项和为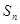 ,数列
,数列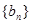 是等比数列,首项
是等比数列,首项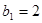 ,且
,且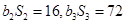 .
.
(1)求数列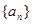 和
和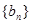 的通项公式;
的通项公式;
(2)令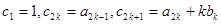 ,其中
,其中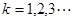 ,求数列
,求数列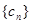 的前
的前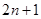 项和
项和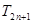 .
.
某区体育局组织篮球技能大赛,每名选手都要进行运球、传球、投篮三项比赛,每名选手在各项比赛中获得合格与不合格的机会相等,且互不影响.现有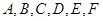 六名选手参加比赛,体育局根据比赛成绩对前
六名选手参加比赛,体育局根据比赛成绩对前 名选手进行表彰奖励.
名选手进行表彰奖励.
(1)求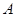 至少获得一个合格的概率;
至少获得一个合格的概率;
(2)求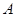 与
与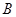 只有一个受到表彰奖励的概率.
只有一个受到表彰奖励的概率.
已知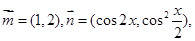 且
且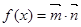 .
.
(1)在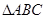 中,若
中,若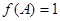 ,求
,求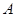 的大小;
的大小;
(2)若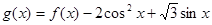 ,将
,将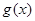 图像上所有点的纵坐标不变,横坐标伸长到原来的
图像上所有点的纵坐标不变,横坐标伸长到原来的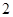 倍,得到
倍,得到 的图像,求
的图像,求 的单调减区间.
的单调减区间.
已知函数 ,
, .
.
(1)设 ,求
,求 的单调区间;
的单调区间;
(2)若对 ,总有
,总有 成立.
成立.
(1)求 的取值范围;
的取值范围;
(2)证明:对于任意的正整数 ,不等式
,不等式
 恒成立.
恒成立.
已知椭圆 的中心在原点,焦点在
的中心在原点,焦点在 轴上,它的一个顶点恰好经过抛物线
轴上,它的一个顶点恰好经过抛物线 的准线,且经过点
的准线,且经过点 .
.
(1)求椭圆 的方程;
的方程;
(2) 若直线
若直线 的方程为
的方程为 .
. 是经过椭圆左焦点
是经过椭圆左焦点 的任一弦,设直线
的任一弦,设直线 与直线
与直线 相交于点
相交于点 ,记
,记 的斜率分别为
的斜率分别为 .试探索
.试探索 之间有怎样的关系式?给出证明过程.
之间有怎样的关系式?给出证明过程.