.(本题14分)在数列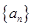 中,
中,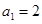 ,
,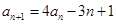 ,
,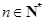 .
.
(Ⅰ)证明数列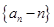 是等比数列;
是等比数列;
(Ⅱ)求数列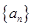 的前
的前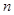 项和
项和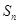 .
.
在直接坐标系
中,直线
的方程为
,曲线
的参数方程为
.
(I)已知在极坐标(与直角坐标系
取相同的长度单位,且以原点
为极点,以x轴正半轴为极轴)中,点
的极坐标为
,判断点
与直线
的位置关系;
(II)设点
是曲线
上的一个动点,求它到直线
的距离的最小值.
设矩阵
(其中
).
(I)若
,求矩阵M的逆矩阵
;
(II)若曲线
在矩阵M所对应的线性变换作用下得到曲线
,求
的值.
如图,四棱锥 中, 底面 ,四边形 中, .
(I)求证:平面
平面
;
(II)设
.
(i)若直线
与平面
所成的角为
,求线段
的长;
(ii)在线段
上是否存在一个点
,使得点
到点
的距离都相等?说明理由.

某产品按行业生产标准分成8个等级,等级系数
依次为1,2,……,8,其中
为标准
,
为标准
,已知甲厂执行标准
生产该产品,产品的零售价为6元/件;乙厂执行标准
生产该产品,产品的零售价为4元/件,假定甲、乙两厂得产品都符合相应的执行标准
(I)已知甲厂产品的等级系数
的概率分布列如下所示:

且
的数字期望
=6,求
的值;
(II)为分析乙厂产品的等级系数
,从该厂生产的产品中随机抽取30件,相应的等级系数组成一个样本,数据如下:
3 5 3 3 8 5 5 6 3 4
6 3 4 7 5 3 4 8 5 3
8 3 4 3 4 4 7 5 6 7
用这个样本的频率分布估计总体分布,将频率视为概率,求等级系数
的数学期望.
(III)在(I)、(II)的条件下,若以"性价比"为判断标准,则哪个工厂的产品更具可购买性?说明理由. 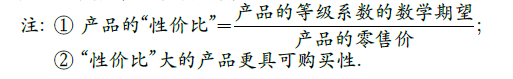
已知等比数列
的公比
,前3项和
。
(I)求数列
的通项公式;
(II)若函数
在
处取得最大值,且最大值为
,求函数
的解析式.