设函数f(x)=ax3+bx2+cx在x=1和x=﹣1处有极值,且f(1)=﹣1,求a,b,c的值,并求出相应的极值.
(本小题满分13分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量 (吨)与相应的生产能耗
(吨)与相应的生产能耗 (吨标准煤)的几组对照数据:
(吨标准煤)的几组对照数据:
 |
3 |
4 |
5 |
6 |
 |
2.5 |
3 |
4 |
4.5 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出 关于
关于 的线性回归方程;
的线性回归方程;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值: )
)
(本小题满分10分)某校高一年级开设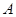 ,
, ,
, ,
,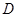 ,
,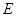 五门选修课,每位同学须彼此独立地选三门课程,其中甲同学必选
五门选修课,每位同学须彼此独立地选三门课程,其中甲同学必选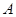 课程,不选
课程,不选 课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.
课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.
(Ⅰ)求甲同学选中 课程且乙同学未选中
课程且乙同学未选中 课程的概率;
课程的概率;
(Ⅱ)用 表示甲、乙、丙选中
表示甲、乙、丙选中 课程的人数之和,求
课程的人数之和,求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分10分)已知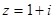 ;
;
(1)如果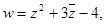 求
求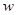 的值;
的值;
(2)如果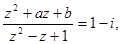 求实数
求实数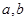 的值.
的值.
(本小题满分13分)已知函数 .
.
(1)若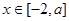 ,求
,求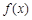 的值域;
的值域;
(2)若存在实数t,当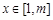 ,
,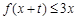 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
(本小题满分13分)某校高一年级开设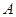 ,
,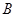 ,
,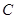 ,
,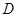 ,
,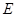 五门选修课,每位同学须彼此独立地选三门课程,其中甲同学必选
五门选修课,每位同学须彼此独立地选三门课程,其中甲同学必选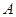 课程,不选
课程,不选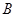 课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.
课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.
(Ⅰ)求甲同学选中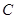 课程且乙同学未选中
课程且乙同学未选中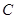 课程的概率;
课程的概率;
(Ⅱ)用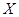 表示甲、乙、丙选中
表示甲、乙、丙选中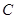 课程的人数之和,求
课程的人数之和,求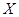 的分布列和数学期望.
的分布列和数学期望.