某企业在第1年初购买一台价值为120万元的设备M,M的价值在使用过程中逐年减少,从第2年到第6年,每年初M的价值比上年初减少10万元;从第7年开始,每年初M的价值为上年初的75%.
(I)求第n年初M的价值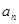 的表达式;
的表达式;
(II)设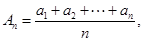 若
若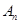 大于80万元,则M继续使用,否则须在第n年初对M更新,证明:必须在第9年初对M进行更新.
大于80万元,则M继续使用,否则须在第n年初对M更新,证明:必须在第9年初对M进行更新.
本题满分12分)已知数列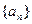 满足
满足 ,
,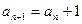 .
.
(1)求数列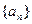 的通项公式;
的通项公式;
(2)设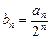 ,求数列
,求数列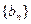 的前n项和Tn.
的前n项和Tn.
已知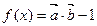 ,其中向量
,其中向量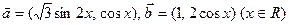 .
.
(1)求函数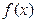 的最小正周期;
的最小正周期;
(2)当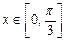 时,求函数
时,求函数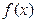 的值域.
的值域.
求平行于直线 ,且与它的距离为
,且与它的距离为 的直线的方程。
的直线的方程。
(本小题满分12分)
已知函数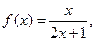 数列
数列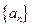 满足
满足 .
.
(1)求证:数列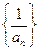 是等差数列;
是等差数列;
(2)若数列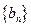 前
前 项和为
项和为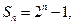 记
记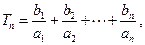 求
求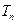 .
.
(本小题满分12分)
在海岸A处,发现北偏东 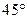 方向,距离A为
方向,距离A为 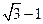
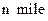 的B处有一艘走私船,在A处北偏西
的B处有一艘走私船,在A处北偏西 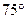 方向,距离A为
方向,距离A为 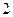
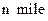 的C处有一艘缉私艇奉命以
的C处有一艘缉私艇奉命以 
 的速度追截走私船,此时,走私船正以
的速度追截走私船,此时,走私船正以 
 的速度从B处向北偏东
的速度从B处向北偏东 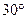 方向逃窜,问缉私艇沿什么方向行驶才能最快追上走私船?并求出所需时间.(本题解题过程中请不要使用计算器,以保证数据的相对准确和计算的方便)
方向逃窜,问缉私艇沿什么方向行驶才能最快追上走私船?并求出所需时间.(本题解题过程中请不要使用计算器,以保证数据的相对准确和计算的方便)
|
|