(本小题满分12分)在数列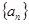 中,
中,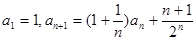
(1)设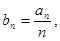 求数列
求数列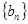 的通项公式;
的通项公式;
(2)求数列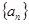 的前
的前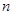 项和
项和
已知椭圆的中心在原点,焦点在x轴上,椭圆的短轴端点和焦点所围成的四边形的正方形,且椭圆上的点到焦点的距离的最大值为 +1,
+1,
(1)求椭圆的标准方程
(2)过椭圆的左焦点F且不与坐标轴垂直的直线交椭圆于A、B两点,线段AB的垂直平分线与x轴交于G点,求G点的横坐标的取值范围
以下茎叶图记录了甲乙两组各四名同学的植树棵数,乙组记录中有一个数据模糊,无法确认,在图中用x表示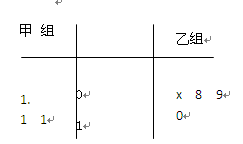
(1)如果x=8,求乙组同学植树棵树的平均数与方差
(2)如果x=9,分别从甲、乙两组中随机选取一名同学,求这两名同学植树总棵数为19的概率 (注:标准差s=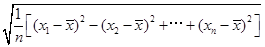 )
)
已知顶点在原点,焦点在x轴上的抛物线过点(1.2)
(1)求抛物线的标准方程
(2)直线y=x-4与抛物线相交于AB两点,求证:OA⊥OB
已知命题p:x2+2x-15≤0,命题q:︱x-1︱≤m (m>0),若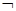 p是
p是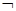 q的必要不充分条件,求实数m的取值范围
q的必要不充分条件,求实数m的取值范围
已知中心在原点,焦点在x轴的椭圆的离心率为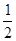 ,椭圆上一点P到两个焦点的距离之和为8,
,椭圆上一点P到两个焦点的距离之和为8,
(1)求椭圆的方程
(2)求与上述椭圆共焦点,且一条渐近线为y=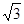 x的双曲线方程
x的双曲线方程