．(本题满分14分) 本题共有2个小题，第1小题满分6分，第2小题满分8分.
如图所示的自动通风设施．该设施的下部
是等腰梯形，其中
米，梯形的高为
米，
米，上部
是个半圆，固定点
为
的中点．△
是由电脑控制其形状变化的三角通风窗（阴影部分均不通风），
是可以沿设施边框上下滑动且始终保持和平行的伸缩横杆．
（1）设与
之间的距离为
米，试将三角通风窗的通风面积
（平方米）表示成关于的函数
；
（2）当与之间的距离为多少米时，三角通风窗的通风面积最大？并求出这个最大面积。
设函数
，曲线
通过点(0，2a+3)，且在
处的切线垂直于y轴．
(I)用a分别表示b和c；
(II)当bc取得最大值时，写出的解析式；
(III)在(II)的条件下，g(x)满足
，求g(x)的最大值及相应x值．
已知a，b，c分别为
ABC的三个内角A，B，C的对边，向量
=(sinA，1)，
=(cosA，
)，且//．
(I)求角A的大小；
(II)若a=2，b=2
，求ABC的面积．
给定椭圆C：
，若椭圆C的一个焦点为F(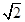
，0)，其短轴上的一个端点到F的距离为
．
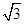(I)求椭圆C的方程；
(II)已知斜率为k(k≠0)的直线l与椭圆C交于不同的两点A，B，点Q满足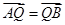
且
=0，其中N为椭圆的下顶点，求直线在y轴上截距的取值范围．
设函数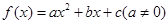
，曲线
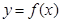通过点(0，2a+3)，且在
处的切线垂直于y轴．
(I)用a分别表示b和c；
(II)当bc取得最大值时，写出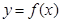的解析式；
(III)在(II)的条件下，若函数
g(x)为偶函数,且当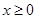
时,
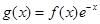，求当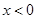
时g(x)的表达式，并求函数g(x)在R上的最小值及相应的x值．
已知数列{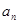
}中，
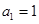，前n项和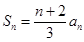
．
(I)求a2，a3以及{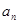}的通项公式；
(II)设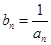
，求数列{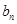
}的前n项和Tn．