在椭圆 中,
中, 为椭圆上的一点,过坐标原点
为椭圆上的一点,过坐标原点 的直线交椭圆于
的直线交椭圆于 两点,其中
两点,其中 在第一象限,过
在第一象限,过 作
作 轴的垂线,垂足为
轴的垂线,垂足为 ,连接
,连接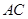 ,
,
(1)若直线 与
与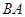 的斜率均存在,问它们的斜率之积是否为定值,若是,求出这个定值,若不是,说明理由;
的斜率均存在,问它们的斜率之积是否为定值,若是,求出这个定值,若不是,说明理由;
(2)若 为
为 的延长线与椭圆的交点,求证:
的延长线与椭圆的交点,求证: .
.
(本小题满分14分)如图,两县城A和B相距20km,现计划在两县城外以AB为直径的半圆弧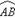 上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为
上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为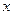 km,建在C处的垃圾处理厂对城A和城B的总影响度为
km,建在C处的垃圾处理厂对城A和城B的总影响度为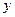 ,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k ,当垃圾处理厂建在
,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k ,当垃圾处理厂建在 的中点时,对城A和城B的总影响度为0.065.
的中点时,对城A和城B的总影响度为0.065.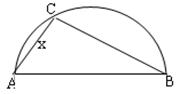
(I)将 表示成
表示成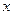 的函数;
的函数;
(II)讨论(1)中函数的单调性,并判断弧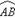 上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由。
上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由。
(本小题满分14分)已知椭圆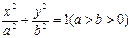 的左右焦点分别为F1、F2,点P在椭圆C上,且PF1⊥F1F2, |PF1|=
的左右焦点分别为F1、F2,点P在椭圆C上,且PF1⊥F1F2, |PF1|=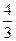 , |PF2|=
, |PF2|=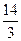 .
.
(I)求椭圆C的方程;
(II)若直线L过圆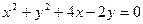 的圆心M交椭圆于A、B两点,且A、B关于点M对称,求直线L的方程。
的圆心M交椭圆于A、B两点,且A、B关于点M对称,求直线L的方程。
(本小题满分14分)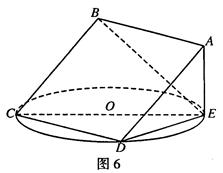
如图6,正方形ABCD所在平面与圆O所在平面
相交于CD,线段CD为圆O的弦,AE垂直于圆
O所在平面,垂足E是圆O上异于C、D的点,
AE=3,圆O的直径为9.
(1)求证:平面 ABCD ⊥平面 ADE;
(2)求二面角D—BC—E的平面角的正切值.
(本小题满分12分)
某公司为庆祝元旦举办了一次抽奖活动,现场准备的抽奖箱里放置了分别标有数字1000、800、600、0的四个球(球的大小相同).参与者随机从抽奖箱里摸取一球(取后即放回),公司即赠送与此球上所标数字等额的奖金(元),并规定摸到标有数字0的球时可以再摸一次,但是所得奖金减半(若再摸到标有数字0的球就没有第三次摸球机会),求一个参与抽奖活动的人可得奖金的期望值是多少元.
(本小题满分12分)
某公司近年来科研费用支出 万元与公司所获得利润
万元与公司所获得利润 万元之间有如下的统计数据:
万元之间有如下的统计数据:
 |
2 |
3 |
4 |
5 |
 |
18 |
27 |
32 |
35 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出 关于
关于 的线性回归方程
的线性回归方程 ;
;
(3)试根据(2)求出的线性回归方程,预测该公司科研费用支出为10万元时公司所获得的利润.
参考公式: