已知椭圆的两焦点为 ,
, ,离心率
,离心率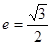 .
.
(1)求此椭圆的方程;
(2)设直线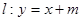 ,若
,若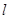 与此椭圆相交于
与此椭圆相交于
 ,
,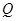 两点,且
两点,且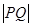 等于椭圆的短轴长,求
等于椭圆的短轴长,求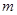 的值;
的值;
(本小题10分)已知 的三个顶点
的三个顶点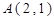 、
、 、
、 ,求
,求
(1) 边所在直线的一般式方程.
边所在直线的一般式方程.
(2) 边上的高
边上的高 所在的直线的一般式方程.
所在的直线的一般式方程.
已知函数 在
在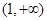 上为增函数,函数
上为增函数,函数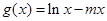
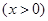 在
在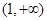 上为减函数.
上为减函数.
(1)分别 求出函数
求出函数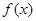 和
和 的导函数;
的导函数;
(2)求实数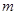 的值;
的值;
(3)求证:当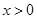 时,
时, 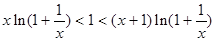
一艘小船在航行中的燃料费和它的速度的立方成正比。已知在速度为每小时10公里时的燃料费是每小时6元,而其他与速度无关的费用是每小时96元。问:此船以多大的速度航行时,能使每公里的费用最少?
已知:椭圆C的中心在原点,焦点在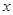 轴上,焦距为8,且经过点(0,3)
轴上,焦距为8,且经过点(0,3)
(1)求此椭圆的方程
若已知直线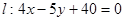 ,问:椭圆C上是否存在一点,使它到直线
,问:椭圆C上是否存在一点,使它到直线 的距离最小?最小距离是多少?
的距离最小?最小距离是多少?
在边长为2的正方体 中,E是BC的中点, F是
中,E是BC的中点, F是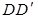 的中点
的中点
(1)求证:CF∥平面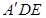
求二面角 的平面角的余弦值。
的平面角的余弦值。