(6分)如图所示的几何体是由几个相同的正方体搭成的, 请画出它的三视图.
一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题: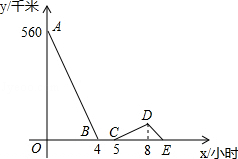
(1)甲乙两地之间的距离为 千米;
(2)求快车和慢车的速度;
(3)求线段DE所表示的y与x之间的函数关系式,并写出自变量x的取值范围.
我国实施“限塑令”后,开始有偿使用环保购物袋.为了满足市场需求,某厂家生产 两种款式的布质环保购物袋,每天共生产4500个,两种购物袋的成本和售价如下表,设每天生产
两种款式的布质环保购物袋,每天共生产4500个,两种购物袋的成本和售价如下表,设每天生产 种购物袋
种购物袋 个,每天共获利
个,每天共获利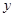 元.
元.
| 成本(元/个) |
售价(元/个) |
|
 |
2 |
2.3 |
 |
3 |
3.5 |
(1)求出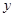 与
与 的函数关系式;
的函数关系式;
(2)如果该厂每天最多投入成本10000元,那么每天最多获利多少元?
为丰富学生的学习生活,某校九年级组织学生参加春游活动,所联系的旅行社收费标准如下: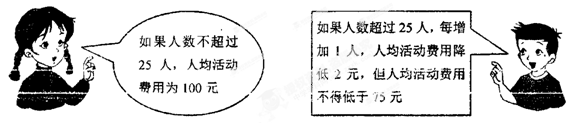
春游活动结束后,该班共支付给该旅行社活动费用2800元,请问该班共有多少人参加这次春游活动?
根据国家发改委实施“阶梯电价”的有关文件要求,某市结合地方实际,决定从今年5月1日起对居民生活用电试行“阶梯电价”收费,具体收费标准见下表:
| 一户居民一个月用电量的范围 |
电费价格(单位:元/千瓦时) |
| 不超过150千瓦时的 |
a |
| 超过150千瓦时,但不超过300千瓦时的部分 |
b |
| 超过300千瓦时的部分 |
a+0.3 |
今年5月份,该市居民甲用电100千瓦时,交电费60元;居民乙用电200千瓦时,交电费122.5元.设该市一户居民在2012年5月以后,某月用电x千瓦时,当月交电费y元.
(1)上表中,a=________;b=________;
(2)请直接写y与x之间的函数关系式;
(3)试行“阶梯电价”收费以后,该市一户居民月用电多少千瓦时时,其当月的平均电价每千瓦时不超过0.62元?
暑期中,哥哥和弟弟二人分别编织28个中国结,已知弟弟单独编织一周(7天)不能完成,而哥哥单独编织不到一周就已完成.哥哥平均每天比弟弟多编2个.
求:(1)哥哥和弟弟平均每天各编多少个中国结?(答案取整数)
(2)若弟弟先工作2天,哥哥才开始工作,那么哥哥工作几天,两人所编中国结数量相同?