（本题满分10分)有一种葡萄：从树上摘下后不保鲜最多只能存放一周，如果放在冷藏室，可以延长保鲜时间，但每天仍有一定数量的葡萄变质，假设保鲜期内的重量基本保持不变，现有一位个体户，按市场价收购了这种葡萄200千克放在冷藏室内，此时市场价为每千克2元，据测算，此后每千克鲜葡萄的市场价格每天可以上涨0．2元，但是，存放一天需各种费用20元，平均每天还有1千克葡萄变质丢弃．(1)存放x天后将鲜葡萄一次性出售，设鲜葡萄的销售金额为y元，写出y关于x的函数关系式；
(2)为了使鲜葡萄的销售金额为760元，又为了尽早清空冷藏室，则需要在几天后一次性出售完；
(3)问个体户将这批葡萄存放多少天后一次性出售，可获得最大利润?最大利润是多少?(本题不要求写出自变量x的取值范围)
把下列各数：－2．5，－12，
，－（－3），0在数轴上表示出来，并用“<”把它们连接起来．
解方程：
（1）3x-4（2x+5）=x+4；
（2）
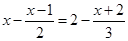
（3）
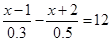
如图，在数轴上（未标出原点及单位长度），点A是线段BC的中点．已知点A、B、C所对应的三个数a、b、c之积是负数，这三个数之和与其中一个数相等，请直接写出求
、
的值．
答：的值是 ，的值是 ．
已知点A在数轴上对应的数为a，点B对应的数为b，且
，A、B之间的距离记作
，
（1）求线段AB的长|AB|；
（2）设点P在数轴上对应的数为x，当|PA|－|PB|＝2时，求x的值；
（3）若点P在点A的左侧，M、N分别是PA、PB的中点，当点P在A的左侧移动时，下列两个结论：①|PM|＋|PN|的值不变；②|PN|－|PM|的值不变，其中只有一个结论正确，请判断出正确结论，并求其值．
一个三角形的第一条边长为（x＋2）cm，第二条边长比第一条边长小5cm，第三条边长是第二条边长的2倍．
（1）用含x的代数式表示这个三角形的周长；
（2）计算当x为6cm时这个三角形的周长．